
return to the main page "Calculus I for Management"
return to the section "Functions & Limits"
Worked-Out Exercises: Functions & Graphs
The following set of exercises is given together with hints, solutions, and solution paths. They are designed such that
you can first try to solve them and in case you need help, please, open the "hints" section. For checking your
answer, please, open the "solution" section and for getting more details or checking your way of solving the
exercise, please, open the "solution path" section.
|
|
|
Exercise 1:
Finding the domain of a function |
| |
|
Find the domain of
\[
f(x) \, \, = \, \, \frac{\sqrt{3-2x}}{x^2+4}
\]
|
|
 Hint Hint
(please, click on the "+" sign to read more)
Recall, the denominator is not allowed to be zero and the argument under a root has to be non-negative.
|
|
 Solution Solution
(please, click on the "+" sign to read more) |
|
 Solution Path Solution Path
(please, click on the "+" sign to read more)
The denominator \(x^2+4\) of \(f(x)\) is always positive, so we need not be concerned
with dividing by \(0\). However, all numbers \(x\) such that \(3-2x<0\) must be excluded
from the domain to prevent taking the square root of a negative number.
Thus, the domain is the set of all numbers \(x\) such that \(3-2x \geq 0\); that is, \(x \leq \tfrac{3}{2}\).
|
|
Exercise 2: Evaluating a cost function |
| |
Suppose the total cost in EUR of manufacturing \(m\) treadmills is given by the function
\(C(m)=m^3-30m^2+500m+200\).
\({\bf{a)}}\) Find the cost of manufacturing \(10\) treadmills. What is the average cost of producing
these treadmills?
\({\bf{b)}}\) Compute the cost of manufacturing the \(10\)th treadmill (marginal cost).
|
|
 Hint Hint
(please, click on the "+" sign to read more)
Recall, that the marginal cost is the cost added by producing one additional unit of a product.
|
|
 Solution Solution
(please, click on the "+" sign to read more)
\({\bf{a)}}\) Cost of manufacturing \(10\) treadmills is \(3200\) EUR; The average cost is \(320\) EUR.
\({\bf{b)}}\) The cost of \(10\)th unit is \(201\) EUR.
|
|
 Solution Path Solution Path
(please, click on the "+" sign to read more)
\({\bf{a)}}\) The cost of manufacturing \(10\) treadmills is the value of the total cost function \(C(m)\)
when \(m=10\); that is,
\[
C(10) \, \, = \, \, 10^3 - 30 \cdot 10^2 + 500 \cdot 10 + 200 \, \, = \, \, 3200 \,.
\]
The average cost of producing the \(10\) treadmills is
\[
AC(10) \, \, = \, \, \frac{C(10)}{10} \, \, = \, \, \frac{3200}{10} \, \, = \, \, 320 \, .
\]
So the total cost of producing \(10\) treadmills is \(3200\) EUR, and the average cost is
\(320\) EUR per treadmill.
\({\bf{b)}}\) The cost of manufacturing the \(10\)th treadmill is the difference between the cost
of manufacturing \(10\) treadmills and the cost of manufacturing \(9\) treadmills:
\begin{eqnarray*}
{\text{cost of \(10\)th treadmill}} & = & C(10) - C(9) \, \, = \, \, 3200 - 2999 \\[1mm]
& = & 201 \quad \text{[EUR]} \,.
\end{eqnarray*}
|
|
Exercise 3: Finding functions that form a given composition |
| |
|
Find functions \(g(u)\) and \(h(x)\) such that \(f(x) = g(h(x))\), where
\[
f(x) \, \, = \, \, \frac{5}{x-2} + 4(x-2)^3 \,.
\]
|
|
 Hint Hint
(please, click on the "+" sign to read more)
Notice, that the form of the given function is
\(
\ f(x) \, \, = \, \, \frac{5}{{\Box}} + 4 \cdot ({\Box})^3 \, ,
\)
|
|
 Solution Solution
(please, click on the "+" sign to read more)
\[
g(u) = \tfrac{5}{u} + 4u^3 \]
\[h(x) = x-2\]
|
|
 Solution Path Solution Path
(please, click on the "+" sign to read more)
The form of the given function is
\[
f(x) \, \, = \, \, \frac{5}{{{\Box}}} + 4 \cdot ({{\Box}})^3 \, ,
\]
where each box \({{\Box}}\) contains the expression \({x-2}\). Thus, \(f(x) = g({{h(x)}})\), where
\[
\underbrace{g(u) = \tfrac{5}{u} + 4u^3}_{\text{outer function}} \qquad \text{and} \qquad
\underbrace{{h(x) = x-2}}_{\text{inner function}} \,.
\]
|
|
Exercise 4:
Writing a linear cost function |
| |
|
A manufacturer's total cost consists of a fixed overhead of \(200\) plus production costs
of \(50\) per unit. Express the total cost as a function of the number of units produced,
and draw the graph.
|
|
 Hint Hint
(please, click on the "+" sign to read more)
Recall, that \[
\text{total cost} \, \, = \, \, (\text{cost per unit}) \cdot (\text{number of units}) + \text{overhead}
\]
|
|
 Solution Solution
(please, click on the "+" sign to read more)
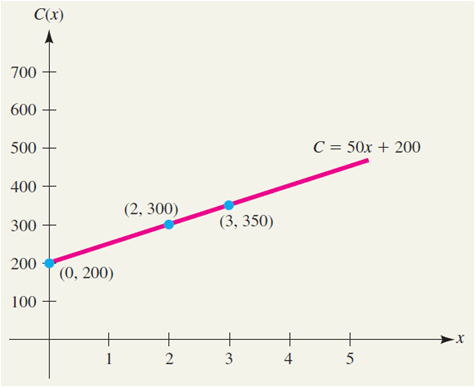
\(C(x) \, \, = \, \, 50x + 200 \,\).
|
|
 Solution Path Solution Path
(please, click on the "+" sign to read more)
Let \(x\) denote the number of units produced and \(C(x)\) the corresponding total cost. Then,
\[
\text{total cost} \, \, = \, \, (\text{cost per unit}) \cdot (\text{number of units}) + \text{overhead}
\]
where the cost per unit is \(50\), the number of units are \(x\), and the overhead is \(200\).
Hence,
\[
C(x) \, \, = \, \, 50x + 200 \, .
\]
The graph of this linear cost function is the line shown in the figure with
- slope \(m=50\) equal to the constant increase in cost per unit of production and
- \(y\)-intercept \((0,200)\) corresponding to the overhead.

|
|
Exercise 5: Modeling with a piecewise-defined function |
| |
During a drought, residents were faced with a severe water shortage. To discourage excessive use of water, the
water district initiated drastic rate increases. The monthly rate for a family of four was \(1.22\) GEL per
\(100\) cubic meter of water for the first \(1200\) cubic meter, \(10\) GEL per \(100\) cubic feet for the
next \(1200\) cubic meter, and \(50\) GEL per \(100\) cubic meter thereafter.
Express the monthly water bill for a family of four as a function of the amount of water used.
|
|
 Hint Hint
(please, click on the "+" sign to read more)
Notice, that you should write system of three equations. When
\(0 \leq x \leq 12\),
\(12 < x \leq 24\), and
\(x > 24\)
|
|
 Solution Solution
(please, click on the "+" sign to read more)
\[
C(x) \, \, = \, \left\{ \begin{array}{l c l}
1.22 x \, , & & \text{if $0 \leq x \leq 12$} \\[1mm]
10x - 105.36 \, , & & \text{if $12 < x \leq 24$} \\[1mm]
50x - 1065.36 \, , & & \text{if $x > 24$}
\end{array} \right.
\]
|
|
 Solution Path Solution Path
(please, click on the "+" sign to read more)
Let \(x\) denote the number of hundred-cubic-meter units of water used by the family during
the month and \(C(x)\) the corresponding cost in GEL. If \(0 \leq x \leq 12\), the cost is
simply the cost per unit times the number of units used:
\[
C(x) \, \, = \, \, 1.22 x
\]
If \(12 < x \leq 24\), each of the first \(12\) units costs \(1.22\) GEL, and so the total cost of
these \(12\) units is \(1.22 \cdot 12 = 14.64\) GEL. Each of the remaining \(x-12\) units costs \(10\) GEL, and hence the total cost of these units is
\(10(x-12)\) GEL. The cost of all \(x\) units is the sum
\[
C(x) \, \, = \, \, 14.64 + 10 (x-12) \, \, = \, \, 10x - 105.36
\]
If \(x > 24\), the cost of the first \(12\) units is \(1.22 \cdot 12 = 14.64\) GEL, the cost of
the next \(12\) units is \(10 \cdot 12 = 120\) GEL, and that of the remaining \(x=24\) units is
\(50(x-24)\) GEL. The cost of all \(x\) units is the sum
\[
C(x) \, \, = \, \, 14.64 + 120 + 50(x-24) \, \, = \, \, 50x - 1065.36 \,.
\]
Combining these three formulas, we can express the total cost as the piecewise-defined
function
\[
C(x) \, \, = \, \left\{ \begin{array}{l c l}
1.22 x \, , & & \text{if $0 \leq x \leq 12$} \\[1mm]
10x - 105.36 \, , & & \text{if $12 < x \leq 24$} \\[1mm]
50x - 1065.36 \, , & & \text{if $x > 24$}
\end{array} \right.
\]
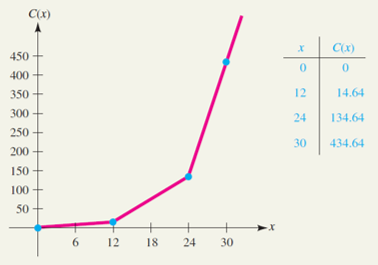
|
|
|
|
Copyright Kutaisi International University — All Rights Reserved — Last Modified: 12/ 10/ 2022
|
|
|

