
return to the main page "Calculus I for Management"
return to the section "Functions & Limits"
Worked-Out Exercises: Limits & Continuity
The following set of exercises is given together with hints, solutions, and solution paths. They are designed such that
you can first try to solve them and in case you need help, please, open the "hints" section. For checking your
answer, please, open the "solution" section and for getting more details or checking your way of solving the
exercise, please, open the "solution path" section.
|
|
|
Exercise 1: Determine the limit if it exists |
| |
|
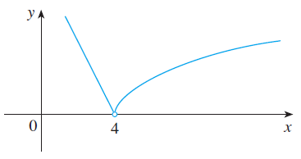
Find \(\lim_{x \to 4} f(x)\) (if it exists) where
$$
f(x) \, \, = \, \left\{ \begin{array}{c c l}
\sqrt{x-4} & & \text{if $x > 4$} \\
8 - 2x & & \text{if $x < 4$}
\end{array} \right.
$$
|
|
 Hint Hint
(please, click on the "+" sign to read more)
First determine one-sided limits. The limit exists if the two one-sided limits have the same value.
|
|
 Solution Solution
(please, click on the "+" sign to read more)
The right-hand and the left-hand side limits are equal. Thus, the limit exists and
$$
\lim_{x \to 4} f(x) \, \, = \, \, 0 \, .
$$
|
|
 Solution Path Solution Path
(please, click on the "+" sign to read more)
 Right-Hand Side Limit:
Right-Hand Side Limit: Since \(f(x) = \sqrt{x-4}\) for \(x > 4\), we have
$$
\lim_{x \to 4^+} f(x) \, \, = \, \, \lim_{x \to 4^+} \sqrt{x-4} \, \, = \, \, \sqrt{4 - 4} \, \, = \, \, 0 \, .
$$
Left-Hand Side Limit: Since \(f(x) = 8 - 2x \) for \(x < 4\), we have
$$
\lim_{x \to 4^-} f(x) \, \, = \, \, \lim_{x \to 4^-} \left( 8 - 2x \right) \, \, = \, \, 8 - 8 \, \, = \, \, 0 \, .
$$
Hence, the right-hand and the left-hand side limits are equal. Thus, the limit exists and
$$
\lim_{x \to 4} f(x) \, \, = \, \, 0 \, .
$$
|
|
Exercise 2: Evaluating a limit |
| |
Determine the following limits (if it exists, or the way it does not exist)
$$
\lim_{x \to 0} \, \frac{\sqrt{1+x} - \sqrt{1-x}}{x} \, .
$$
|
|
 Hint Hint
(please, click on the "+" sign to read more)
Apply the Third Binomial Formula after multiplying both numerator and denominator by
\(\sqrt{1+x} + \sqrt{1-x}\) (recall, this procedure is called rationalizing).
|
|
 Solution Solution
(please, click on the "+" sign to read more)
\[
\lim_{x \to 0} \, \frac{\sqrt{1+x} - \sqrt{1-x}}{x} \, \, = \, \, 1 \, .
\]
|
|
 Solution Path Solution Path
(please, click on the "+" sign to read more)
\begin{eqnarray*}
\frac{\sqrt{1+x} - \sqrt{1-x}}{x} & = & \frac{\sqrt{1+x} - \sqrt{1-x}}{x} \cdot \frac{\sqrt{1+x} + \sqrt{1-x}}{\sqrt{1+x} + \sqrt{1-x}} \\[1mm]
& = &
\frac{(1+x) - (1-x)}{x \cdot (\sqrt{1+x} + \sqrt{1-x})} \, \, = \, \, \frac{2x}{x \cdot (\sqrt{1+x} + \sqrt{1-x})}\\[1mm]
& = &
\frac{2}{\sqrt{1+x} + \sqrt{1-x}} \, \, \stackrel{x \to 0}{\longrightarrow} \, \, \frac{2}{1+1} \, \, = \, \, 1 \, .
\end{eqnarray*}
|
|
Exercise 3: Infinite limits and vertical asymptotes |
| |
|
Let
$$
f(x) \, \, = \, \, \frac{x^2 - 5x + 6}{x^2 - 2x} \, .
$$
Does the graph of \(f\) have any vertical asymptotes?
|
|
 Hint Hint
(please, click on the "+" sign to read more)
Try to factorize the numerator and check for denominator to be 0.
|
|
 Solution Solution
(please, click on the "+" sign to read more)
The graph of \(f\) has vertical asymptote at \(x = 0\).
|
|
 Solution Path Solution Path
(please, click on the "+" sign to read more)
First, we check if we can factorize the numerator \(x^2 - 5x + 6\). We have
\[
x_{1/2} \, \, = \, \, \frac{5 \pm \sqrt{25-24}}{2} \, \, = \, \, \frac{5 \pm 1}{2} \, \, = \, \left\{ \begin{array}{c}
3 \\ 2 \end{array} \right.
\]
Thus,
\[
\frac{x^2 - 5x + 6}{x^2 - 2x} \, \, = \, \, \frac{(x-3) \cdot (x-2)}{x \cdot (x-2)} \, \, = \, \, \frac{x-3}{x} \qquad \text{for $x \neq 2$} \, ,
\]
such that the graph of \(f\) has a hole at \(x=2\) and a vertical asymptote at \(x = 0\) with (\(x-3 < 0\) for \(x\) close to \(0\))
\[
\lim_{x \to 0^{-}} f(x) \, \, = \, \, \infty \qquad \text{and} \qquad \lim_{x \to 0^{+}} f(x) \, \, = \, \, -\infty
\]
|
|
Exercise 4: Infinite limits at infinity,
roots and \(y\)-intercept to sketch a graph |
| |
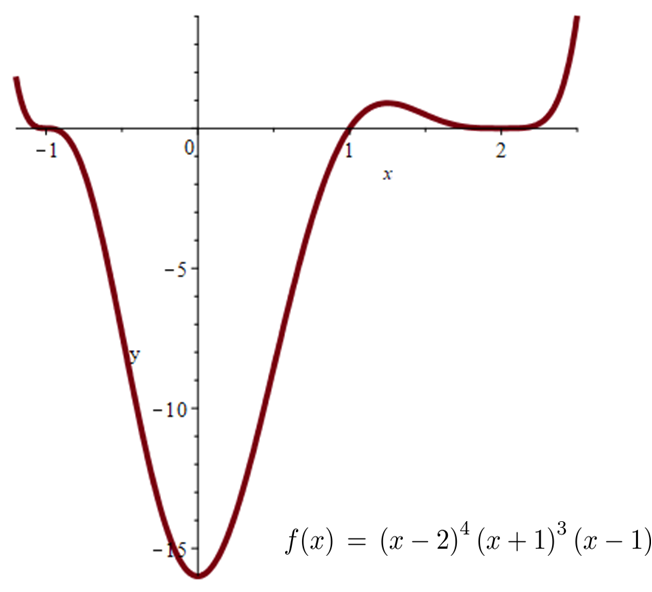
Sketch the graph of
\[
f(x) \, \, = \, \, \left( x-2 \right)^4 \cdot \left( x+1 \right)^3 \cdot \left( x-1 \right)
\]
by finding its roots (\(x\)-intercepts), \(y\)-intercept, and limits at infinity as \(x \to \infty\) and \(x \to -\infty\).
This means:
- Discuss continuity of \(f\).
- Find the \(y\)-intercept, i.e. the value \(f(0)\).
- Find the roots of \(f\), i.e. solve \(f(x) = 0\) for \(x\).
- Discuss the limits at infinity.
|
|
 Hint Hint
(please, click on the "+" sign to read more)
- For the function to be continuous, there mustn't be discontinuities or vertical asymptotes.
- To find \(y\) intercept, plug in 0 to the function.
- To find the roots, calculate \(f(x) = 0\).
- Think about what happens to the function when \(x\) is either large positive or large negative.
|
|
 Solution Solution
(please, click on the "+" sign to read more)
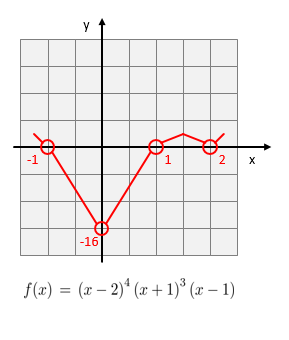
- Continuity: The function is continuous on the whole \(\mathbb{R}\)
- \(y\)-intercept is -16
- Roots: \(x \in \{ 2, -1, 1 \}\) .
- Limits at infinity: Limits at infinity are both infinity.
|
|
 Solution Path Solution Path
(please, click on the "+" sign to read more)
- Continuity: The function is a product of powers of polynomials and thus continuous on the whole of
\(\mathbb{R}\). I.e. there are no discontinuities and vertical asymptotes.
- \(y\)-intercept: \(f(0) = (-2)^4 (1)^3 (-1) = -16\)
- Roots: Due to the product structure, the roots \(f(x) = 0\) are easily found at \(x \in \{ 2, -1, 1 \}\)
\((x-2)^4\) is never negative, hence \(f\) doesn't change sign at \(x=2\) and the graph doesn't cross the \(x\)-axis at \(x = 2\).
The graph crosses the \(x\)-axis at \(x = 1\) and \(x = -1\).
- Limits at infinity:
When \(x\) is large positive, all three factors are large, so
\[
\lim_{x \to \infty} \, \underbrace{\left( x-2 \right)^4}_{\to \, \infty}
\underbrace{\left( x+1 \right)^3}_{\to \, \infty} \underbrace{\left( x-1 \right)}_{\to \, \infty}
\, \, = \, \, \infty \, .
\]
When \(x\) is large negative, the first factor is large positive and the second and third factors are both large negative, so
\[
\lim_{x \to \infty} \, \underbrace{\left( x-2 \right)^4}_{\to \, \infty} \underbrace{\left( x+1 \right)^3}_{\to \, -\infty}
\underbrace{\left( x-1 \right)}_{\to \, -\infty}
\, \, = \, \, \infty \, .
\]
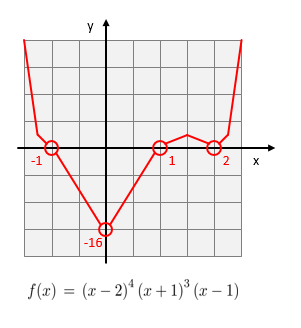
Thus, we get the following sketch of \( f(x) = \left( x-2 \right)^4 \left( x+1 \right)^3 \left( x-1 \right) \):
|
|
Exercise 5: Graphing the function |
| |
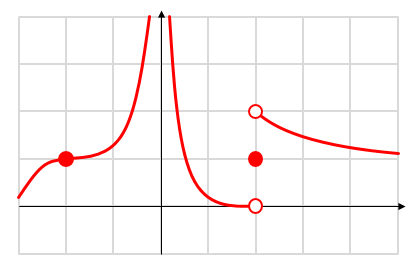
Draw the graph of a function \(y = f(x)\) such that the following properties are satisfied:
- \(\lim\limits_{x \to -2} \, f(x) \, \, = \, \, 1\)
- \(\lim\limits_{x \to 0} \, f(x) \, \, = \, \, \infty\)
- \(\lim\limits_{x \to 2^+} \, f(x) \, \, = \, \, 2\)
- \(\lim\limits_{x \to 2^-} \, f(x) \, \, = \, \, 0\)
- \(f(2) \, \, = \, \, 1\)
- \(\lim\limits_{x \to \infty} \, f(x) \, \, = \, \, 1\)
|
|
 Hint Hint
(please, click on the "+" sign to read more)
Draw the information that you get from the points a.-f. into a common coordinate system. Then, connect the
different peices of information. You may want to use auxiliary lines, like for vertical and horizontal asymptotes,
that you can better fit the graph to the given information.
|
|
 Solution Solution
(please, click on the "+" sign to read more)
We have:
|
|
 Solution Path Solution Path
(please, click on the "+" sign to read more)
The procedure of settig-up the sketch is similar to that of exercise 4 above.
|
|
Exercise 6: A continuous function on a closed interval |
| |
Show that the function \(f(x) = 1 - \sqrt{1-x^2}\) is continuous on the closed interval \([-1,1]\).

|
|
 Hint Hint
(please, click on the "+" sign to read more)
The function is continuous on \([-1,1]\) if it is continuous for all interior and boundary points.
|
|
 Solution & Solution Path Solution & Solution Path
(please, click on the "+" sign to read more)
Step 1: Interior points.
If \(-1 < a < 1\) (i.e. in the interior of the interval where both one-sided limits may exist), then using the limit laws, we have
\begin{eqnarray*}
\lim_{x \to a} f(x) & = & \lim_{x \to a} \left( 1 - \sqrt{1 - x^2} \right) \, \, = \, \, 1 - \lim_{x \to a} \sqrt{1 - x^2}
& = & 1 - \sqrt{ \lim_{x \to a} \left( 1-x^2 \right) } \, \, = \, \, 1 - \sqrt{ 1 - \lim_{x \to a} x^2 }
& = & 1 - \sqrt{ 1 - a^2} \, \, = \, \, f(a) \, .
\end{eqnarray*}
Thus, \(f\) is continuous for all \(a \in (-1, 1)\).
Step 2: Boundary points.
Similar calculations show that
$$
\lim_{x \to -1^+} f(x) \, \, = \, \, 1 \, \, = \, \, f(-1)
$$
and
$$
\lim_{x \to 1^-} f(x) \, \, = \, \, 1 \, \, = \, \, f(1)
$$
so \(f\) is continuous from the right at \(-1\) and continupous from the left at \(1\).
Therefore, \(f\) is continuous on \([-1,1]\).
|
|
Exercise 7: Application of the
intermediate value property (IVP) in locating roots |
| |
Show that there is a root of the equation
\[
f(x) \, \, = \, \, 0 \qquad \text{with} \qquad f(x) \, \, = \, \, 4 x^3 - 6 x^2 + 3 x - 2
\]
between \(1\) and \(2\).
|
|
 Hint Hint
(please, click on the "+" sign to read more)
If either \(f(1)\) or \(f(2)\) is more than 0, while another is less than 0, \(x\) for \(f(x) = 0\) will be between \(1\) and \(2\)
|
|
 Solution & Solution Path Solution & Solution Path
(please, click on the "+" sign to read more)
We are looking for a solution of the given equation, that is, a number \(c \in (1, 2)\) such that \(f(c) = 0\).
Therefore, we take \(a = 1\), \(b = 2\), and \(N = 0\) in the IVP. We have
\[
f(1) \, \, = \, \, 4 - 6 + 3 - 2 \, \, = \, \, -1 \, \, < \, \, 0
\]
and
\[
f(-1) \, \, = \, \, 32 - 24 + 6 - 2 \, \, = \, \, 12 \, \, > \, \, 0 \, .
\]
Thus \(f(1) < 0 < f(2)\); i.e. \(N = 0\) is a number between \(f(1)\) and \(f(2)\).
Now \(f\) is continuous since it is a polnomial, so the IVP says there is a number \(c\) between \(1\) and \(2\) such that \(f(c) = 0\).
In other words, the equation \(4 x^3 - 6 x^2 + 3 x - 2 = 0\) has at least one root \(c\) in the interval \( (1, 2) \).
|
|
|
|
Copyright Kutaisi International University — All Rights Reserved — Last Modified: 12/ 10/ 2022
|
|
|

