Mathematics for Management -- Supplementary Electronic Materials

return to the main page "Calculus I for Management"
return to the section "Differentiation Rules"

Worked-Out Exercises: Advanced Differentiation Rules

The following set of exercises is given together with hints, solutions, and solution paths. They are designed such that you can first try to solve them and in case you need help, please, open the "hints" section. For checking your answer, please, open the "solution" section and for getting more details or checking your way of solving the exercise, please, open the "solution path" section.


Exercise 1: Application of differentiation rules

Differentiate the following functions: \[ {\bf{a)}} \quad f(x) \, = \, \tfrac{7}{4} x^2 - 3x + 12 \, , \quad {\bf{b)}} \quad f(x) \, = \, x^{-3/5} + x^4 \, , \quad {\bf{c)}} \quad f(x) \, = \, \sqrt{x} - 2 {\rm{e}}^x \, , \]

Hint (please, click on the "+" sign to read more) Use Power Rule (multiply the variable's exponent n, by its coefficient, then subtract \(1\) from the exponent.)

Solution (please, click on the "+" sign to read more) a) \(f'(x) = \tfrac{7}{2} x - 3\), b) \(f'(x) = -\tfrac{3}{5} x^{-8/5} + 4 x^3\) c) \(f'(x) = \frac{1}{2 \sqrt{x}} - 2 {\rm{e}}^x\)

Solution Path (please, click on the "+" sign to read more) a) \(f(x) = \tfrac{7}{4} x^2 - 3x + 12\) is a polynomial and we differentiate each term separately making use of the sum/ difference rule, the constant multiple rule and the power rule: \[ f'(x) \, \, = \, \, \underbrace{\frac{\textrm{d}}{\textrm{d} x} \left( \tfrac{7}{4} x^2 \right)}_{= \, \tfrac{7}{4} \cdot 2 \cdot x} - \underbrace{\frac{\textrm{d}}{\textrm{d} x} \left( 3x \right)}_{= \, 3} + \underbrace{\frac{\textrm{d}}{\textrm{d} x} \left( 12 \right)}_{= \, 0} \\[1mm] \, \, = \, \, \tfrac{7}{2} x - 3 \, . \] b) \(f(x) = x^{-3/5} + x^4\) is the sum of two power functions and we differentiate each term separately again making use of the sum rule and the power rule: \[ f'(x) \, \, = \, \, \underbrace{\frac{\textrm{d}}{\textrm{d} x} \left( x^{-3/5} \right)}_{= \, -\tfrac{3}{5} \cdot x^{-8/5}} + \underbrace{\frac{\textrm{d}}{\textrm{d} x} \left( x^4 \right)}_{= \, 4 \cdot x^3} \, \, = \, \, -\tfrac{3}{5} x^{-8/5} + 4 x^3 \, . \] b) For \(f(x) = \sqrt{x} - 2 {\rm{e}}^x\) we also differentiate each term separately making use of the sum/ difference rule, the constant multiple rule, the rule for exponentials, and the power rule (with \(x^{1/2} = \sqrt{x}\)): \[ f'(x) \, \, = \, \, \underbrace{\frac{\textrm{d}}{\textrm{d} x} \left( x^{1/2} \right)}_{= \, \tfrac{1}{2} \cdot x^{-1/2}} - \underbrace{\frac{\textrm{d}}{\textrm{d} x} \left( 2 {\rm{e}}^x \right)}_{= \, 2 {\rm{e}}^x } \, \, = \, \, \frac{1}{2 \sqrt{x}} - 2 {\rm{e}}^x \, . \]

Exercise 2: Connecting derivatives and graphs

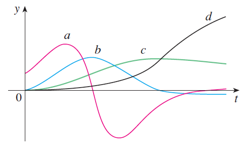
The figure shows the graphs of four functions. One is the position function \(s(t)\) of a car, one is the velocity \(\dot{s}(t)\) of the car, one is its acceleration \(\ddot{s}(t)\), and one is its jerk \(s^{(3)}(t)\). Identify each curve and explain your choices.

Hint (please, click on the "+" sign to read more) Velocity is the rate of change of position Acceleration is the rate of change of velocity Jerk is the rate of change of acceleration

Solution (please, click on the "+" sign to read more) We have that: Graph d is that of the position function \(s(t)\) Graph c is that of the velocity function \(v(t) = \dot{s}(t)\) Graph b is that of the acceleration function \(a(t) = \ddot{s}(t)\) Graph a is that of the jerk function \(j(t) = s^{(3)}(t)\)

Solution Path (please, click on the "+" sign to read more) Based on how strong the graph of d increases, we see that c is the graph of its derivative. Based on the inclination behavior, we have that the graph of b is that of the derivative of c . From the previous problem, we have that graph a is the graph of the derivative of b .

Exercise 3: Application of the product rule

Let \(f(x) = \sqrt{x} \cdot g(x)\), where \(g(4) = 2\) and \(g'(4) = 3\). Determine the value of \(f'(4)\).

Hint (please, click on the "+" sign to read more) Apply Product Rule (derivative of a product of two functions is the first function multiplied by the derivative of the second function plus the second function multiplied by the derivative of the first function).

Solution (please, click on the "+" sign to read more) \( f'(4) \, \, = \, \, \sqrt{4} \cdot g'(4) + \frac{g(4)}{2 \cdot \sqrt{4}} \, \, = \, \, 2 \cdot 3 + \frac{2}{2 \cdot 2} \, \, = \, \, 6.5 \, .\)

Solution Path (please, click on the "+" sign to read more) By applying the Product Rule, we obtain \begin{eqnarray} f'(x) & = & \frac{\textrm{d}}{\textrm{d} \, x} \left( \sqrt{x} \cdot g(x) \right) \, \, = \, \, \sqrt{x} \, \, \frac{\textrm{d} \, g(x)}{\textrm{d} \, x} \, + \, g(x) \, \frac{\textrm{d} \, \sqrt{x}}{\textrm{d} \, x} \\[2mm] & = & \sqrt{x} \cdot g'(x) + \frac{g(x)}{2 \cdot \sqrt{x}} \, . \end{eqnarray} Thus: \[ f'(4) \, \, = \, \, \sqrt{4} \cdot g'(4) + \frac{g(4)}{2 \cdot \sqrt{4}} \, \, = \, \, 2 \cdot 3 + \frac{2}{2 \cdot 2} \, \, = \, \, 6.5 \, . \]

Exercise 4: Product ↦ quotient rule

Differentiate the following functions: \[ {\bf{a)}} \quad f(x) \, = \, ({\rm{e}}^x + 2)(2 {\rm{e}}^x - 1) \, , \qquad \text{and} \qquad {\bf{b)}} \quad f(x) \, = \, \frac{6 x^4 - 5 x}{x+1} \, . \]

Hint (please, click on the "+" sign to read more) The Product Rule says that the derivative of a product of two functions is the first function multiplied by the derivative of the second function plus the second function multiplied by the derivative of the first function. The Quotient Rule says that the derivative of a quotient is the denominator multiplied by the derivative of the numerator minus the numerator multiplied by the derivative of the denominator and all divided by the square of the denominator.

Solution (please, click on the "+" sign to read more) a) \( f'(x) = 4 {\rm{e}}^{2x} + 3 {\rm{e}}^x \) b) \( f'(x) = \frac{18 x^4 + 24 x^3 -5}{(x+1)^2} \)

Solution Path (please, click on the "+" sign to read more) a) \begin{eqnarray} f'(x) & = & {\rm{e}}^x (2 {\rm{e}}^x - 1) + 2 {\rm{e}}^x ({\rm{e}}^x + 2) \\[2mm] & = & {\rm{e}}^x (4 {\rm{e}}^x + 3)\\[2mm] & = & 4 {\rm{e}}^{2x} + 3 {\rm{e}}^x \end{eqnarray} b) \begin{eqnarray} f'(x) & = & \frac{(24x^3-5)(x+1)-(6x^4-5x)}{(x+1)^2} \\[0.8mm] & = & \frac{24 x^4 - 6 x^4 + 24 x^3 - 5x - 5 + 5x}{(x+1)^2} \\[0.8mm] & = & \frac{18 x^4 + 24 x^3 -5}{(x+1)^2} \end{eqnarray}

Exercise 5: Application of the quotient rule

If \(f\) is a differentiable function, find an expression for the derivative of \[ y \, \, = \, \, F(x) \, \, = \, \, \frac{f(x)}{x^2} \, . \]

Hint (please, click on the "+" sign to read more) Apply Quotient Rule (the derivative of a quotient is the denominator multiplied by the derivative of the numerator minus the numerator multiplied by the derivative of the denominator and all divided by the square of the denominator).

Solution (please, click on the "+" sign to read more) \(y '= F'(x) = \frac{x \cdot f'(x) - 2 f(x)}{x^3} \ \)

Solution Path (please, click on the "+" sign to read more) By virtue of the Quotient Rule, we have: \[ F'(x) \, \, = \, \, \frac{x^2 \cdot f'(x) - 2x \cdot f(x)}{x^4} \, \, = \, \, \frac{x \cdot f'(x) - 2 f(x)}{x^3} \, , \] where \(f'\) is the derivative of \(f\).