
return to the main page "Calculus I for Management"
return to the section "Applications of Differentiation"
Worked-Out Exercises: Applications of Differentiation
The following set of exercises is given together with hints, solutions, and solution paths. They are designed such that
you can first try to solve them and in case you need help, please, open the "hints" section. For checking your
answer, please, open the "solution" section and for getting more details or checking your way of solving the
exercise, please, open the "solution path" section.
|
|
|
Exercise 1: Application of the Chain Rule
|
| |
|
Differentiate \({\bf{a)}}\) \(y = (x^3 - 1)^{100}\) and \({\bf{b)}}\) \(y = (2x+1)^5 (x^3-x+1)^4\) .
|
|
 Hint Hint
(please, click on the "+" sign to read more)
Recall, that \(F'(x) \, \, = \, \, f'( g(x) ) \cdot g'(x)\).
|
|
 Solution Solution
(please, click on the "+" sign to read more)
\({\bf{a)}}\) \(300 x^2 (x^3-1)^{99}\) .
\({\bf{b)}}\) \(2 (2x+1)^4 (x^3-x+1)^3 (17 x^3 + 6 x^2 - 9x + 3)\).
|
|
 Solution Path Solution Path
(please, click on the "+" sign to read more)
\({\bf{a)}}\) With \(f(u) = u^3\) and \(g(x) = x^3 - 1\) we have
\[
\frac{\textrm{d}}{\textrm{d} \, x} \, (x^3 - 1)^{100} \, \, = \, \, 100 (x^3 - 1)^{99} \cdot 3 x^2 \, \, = \, \, 300 x^2 (x^3-1)^{99} \, .
\]
\({\bf{b)}}\) Here we must use the Product Rule before using the Chain Rule:
\[\begin{eqnarray*}
y' & = & \frac{\textrm{d}}{\textrm{d} \, x} \, (2x+1)^5 (x^3-x+1)^4 \\
& = &
5 (2x+1)^4 \cdot 2 \cdot (x^3-x+1)^4 + (2x+1)^5 \cdot 4 (x^3-x+1)^3 \cdot (3y^2-1) \\
& = &
2 (2x+1)^4 (x^3-x+1)^3 (17 x^3 + 6 x^2 - 9x + 3) \, .
\end{eqnarray*}\]
|
|
Exercise 2: Application of implicit differentiation |
| |
|
Let \(\sin(x+y) = y^2 \cos(x)\). Find \(y'\).
|
|
 Hint Hint
(please, click on the "+" sign to read more)
Use the chain rule for the both sides of the equation and then collect the terms that involve \(y'\).
|
|
 Solution Solution
(please, click on the "+" sign to read more)
\(y' \, \, = \, \, \frac{y^2 \sin(x) + \cos(x+y)}{2y \cos(x) - \cos(x+y)} \,\).
|
|
 Solution Path Solution Path
(please, click on the "+" sign to read more)
Differentiating implicitly with respect to \(x\) and remembering that \(y = y(x)\) is a
function of \(x\), we get
\[
\cos(x+y) \cdot (1 + y') \, \, = \, \, 2y \cdot y' \cdot \cos(x) \, + \, y^2 \cdot (-\sin(x)) \, .
\]
(Note that we have used the Chain Rule on the left side and the Product Rule and Chain
Rule on the right side.) If we collect the terms that involve \(y'\), we get
\[
\cos(x + y) \, + \, y^2 \sin(x) \, \, = \, \, (2y \cos(x)) \cdot y' \, - \, \cos(x+y) \cdot y' \, .
\]
Thus,
\[
y' \, \, = \, \, \frac{y^2 \sin(x) + \cos(x+y)}{2y \cos(x) - \cos(x+y)} \, .
\]
|
|
Exercise 3: Application of implicit differentiation |
| |
|
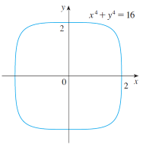
Let \(x^4 + y^4 = 16\). Find \(y''\).
|
|
 Hint Hint
(please, click on the "+" sign to read more)
Differentiate the equation with respect to \(x\), find \(y'\) and differentiate the equation again with respect to \(x\) in order to find \(y''\).
|
|
 Solution Solution
(please, click on the "+" sign to read more)
\(\, \, -48 \frac{x^2}{y^7} \,\).
|
|
 Solution Path Solution Path
(please, click on the "+" sign to read more)
Differentiating the equation implicitly with respect to \(x\), we get
\[
4 x^3 \, + \, 4 y^3 y' \, \, = \, \, 0 \qquad \Longrightarrow \qquad
y' \, \, = \, \, -\frac{x^3}{y^3} \, . \hspace{3cm} \phantom{u}
\]
To find \(y''\) we differentiate this expression for \(y'\) using the Quotient Rule and remembering
that \(y\) is a function of \(x\):
\[\begin{eqnarray*}
y'' & = & \frac{\textrm{d}}{\textrm{d} \, x} \left( -\frac{x^3}{y^3} \right) \, \, = \, \,
-\frac{3 x^2 \cdot y^3 - x^3 \cdot 3y^2 \cdot y'}{y^6}\\[1mm]
& = &
-\frac{3 x^2 \cdot y^3 - x^3 \cdot 3y^2 \cdot \left( -\frac{x^3}{y^3} \right)}{y^6}
\, \, = \, \,
- \frac{3x^2 (x^4 + y^4)}{y^7} \,
\end{eqnarray*} \]
The values of \(x\) and \(y\) must satisfy the original equation \(x^4 + y^4 = 16\). So the answer simplifies to
\[
y'' \, \, = \, \, -\frac{3 x^2 \cdot 16}{y^7} \, \, = \, \, -48 \frac{x^2}{y^7} \, .
\]
|
|
Exercise 4: Application of l'Hospital's Rule |
| |
|
Calculate
\[
\lim_{x \to \infty} \, \frac{{\rm{e}}^x}{x^2} \, .
\]
|
|
 Hint Hint
(please, click on the "+" sign to read more)
Keep in mind, that in some cases you might have to use l'Hospital's Rule more than once.
|
|
 Solution Solution
(please, click on the "+" sign to read more)
\(\lim_{x \to \infty} \, \frac{{\rm{e}}^x}{x^2} \, = \, \, \infty \, .\)
|
|
 Solution Path Solution Path
(please, click on the "+" sign to read more)
We have \(\lim_{x \to \infty} \, {\rm{e}}^x = \infty\) and \(\lim_{x \to \infty} \, x^2 = \infty\), so the limit is an indeterminate form of type \(\frac{\infty}{\infty}\), and l'Hospital's Rule (\(\text{l'H}\)) gives
\[
\lim_{x \to \infty} \, \frac{{\rm{e}}^x}{x^2} \, \, \stackrel{\text{l'H}}{=} \, \,
\lim_{x \to \infty} \, \frac{\, \, \frac{\textrm{d}}{\textrm{d} x} \, {\rm{e}}^x \, \,}{\frac{\textrm{d}}{\textrm{d} x} \, x^2} \, \, = \, \,
\lim_{x \to \infty} \, \frac{{\rm{e}}^x}{2x}
\]
Since \(\lim_{x \to \infty} \, {\rm{e}}^x = \infty\) and \(\lim_{x \to \infty} \, 2x = \infty\), the limit on the right hand side is also an indeterminate form of type \(\frac{\infty}{\infty}\).
A second application of l'Hospital's Rule (\(\text{l'H}\)) gives
\[
\lim_{x \to \infty} \, \frac{{\rm{e}}^x}{x^2} \, \, = \, \, \lim_{x \to \infty} \, \frac{{\rm{e}}^x}{2x}
\, \, \stackrel{\text{l'H}}{=} \, \, \lim_{x \to \infty} \, \frac{{\rm{e}}^x}{2} \, \ = \, \, \infty \, .
\]
|
|
Exercise 5: Application of l'Hospital's Rule on indeterminate powers |
| |
|
Calculate \(\lim_{x \to 0^+} \, \left( 1 + \sin(4x) \right)^{\cot(x)}\).
|
|
 Hint Hint
(please, click on the "+" sign to read more)
Calculate limit for \(\ln(y) \, \, = \, \, \ln\left( \left( 1 + \sin(4x) \right)^{\cot(x)} \right) \, \,\) and recall, that \(y = {\rm{e}}^{\ln(y)}\).
|
|
 Solution Solution
(please, click on the "+" sign to read more)
\(\lim_{x \to 0^+} \, \left( 1 + \sin(4x) \right)^{\cot(x)} = e^4\).
|
|
 Solution Path Solution Path
(please, click on the "+" sign to read more)
First notice that as \(x \to 0^+\), we have \(1+ \sin(4x) \to 1\) and \(\cot(x) \to \infty\), so the given limit is indeterminate (type \(1^{\infty}\)).
Let \(y = \left( 1 + \sin(4x) \right)^{\cot(x)}\). Then
\[
\ln(y) \, \, = \, \, \ln\left( \left( 1 + \sin(4x) \right)^{\cot(x)} \right) \, \, = \, \, \cot(x) \cdot \ln\left( 1 + \sin(4x) \right) \, \, = \, \,
\frac{\ln\left( 1 + \sin(4x) \right)}{\tan(x)}
\]
so l'Hospital's Rule (\(\text{l'H}\)) gives
\[
\lim_{x \to 0^+} \, \ln(y) \, \, = \, \, \lim_{x \to 0^+} \, \frac{\ln\left( 1 + \sin(4x) \right)}{\tan(x)} \, \, \stackrel{\text{l'H}}{=} \, \,
\lim_{x \to 0^+} \, \frac{\, \, \frac{4 \, \cos(4x)}{1 + \sin(4x)} \, \,}{\sec^2(x)} \, \, = \, \, 4
\]
Hence, \(\lim_{x \to 0^+} \, \left( 1 + \sin(4x) \right)^{\cot(x)} = \lim_{x \to 0^+} \, y = \lim_{x \to 0^+} \, {\rm{e}}^{\ln(y)} = {\rm{e}}^4\).
|
|
Exercise 6: Differentials and the quality of linear approximation |
| |
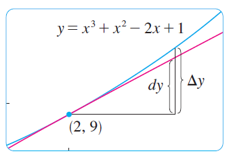
Compare the values of \(\Delta y\) and \(\textrm{d} y\) if \(y = f(x) = x^3 + x^2 - 2x + 1\) and
\(x\) changes \({\bf{a)}}\) from \(2\) to \(2.05\) and \({\bf{b)}}\) from \(2\) to \(2.01\).
|
|
 Hint Hint
(please, click on the "+" sign to read more)
Note, that \(\Delta y = f(x_2) - f(x_1)\) and \(
\textrm{d} y \, \, = \, \, f'(x) \, \textrm{d} x \, \,.
\)
|
|
 Solution Solution
(please, click on the "+" sign to read more)
\({\bf{a)}}\) \(\Delta y = 0.717625 \), \(\textrm{d} y = 0.7\)
\({\bf{b)}}\) \(\Delta y = 0.140701 \), \(\textrm{d} y = 0.14\)
|
|
 Solution Path Solution Path
(please, click on the "+" sign to read more)
We have
\(\begin{eqnarray*}
f(2) & = & 2^3 + 2^2 - 2 \cdot 2 + 1 \, \, = \, \, 9 \\[1mm]
f(2.05) & = & (2.05)^3 + (2.05)^2 - 2 \cdot 2.05 + 1 \, \, = \, \, 9.717625 \\[1mm]
\Delta y & = & f(2.05) - f(2) \, \, = \, \, 0.717625
\end{eqnarray*}\)
In general,
\[
\textrm{d} y \, \, = \, \, f'(x) \, \textrm{d} x \, \, = \, \, (3 x^2 + 2x - 2) \textrm{d} x \, .
\]
When
\(x = 2\) and \(\textrm{d} x = \Delta x = 0.05\), this becomes
\(\begin{eqnarray*}
\textrm{d} y & = & (3 \cdot 2^2 + 2 \cdot 2 - 2) \cdot 0.05 \, \, = \, \, 0.7 \\[1mm]
f(2.01) & = & (2.01)^3 + (2.01)^2 - 2 \cdot 2.01 + 1 \, \, = \, \, 9.140701 \\[1mm]
\Delta y & = & f(2.01) - f(2) \, \, = \, \, 0.140701
\end{eqnarray*}\)
When \(\textrm{d} x = \Delta x = 0.01\),
\[
\textrm{d} y \, \, = \, \, (3 \cdot 2^2 + 2 \cdot 2 - 2) \cdot 0.01 \, \, = \, \, 0.14 \, .
\]
|
|
|
|
Copyright Kutaisi International University — All Rights Reserved — Last Modified: 12/ 10/ 2022
|
|
|

