Mathematics for Management -- Supplementary Electronic Materials

return to the main page "Calculus I for Management"
return to the section "Exponential Functions & Marginal Analysis"

Worked-Out Exercises: Exponential & Logarithmic Functions

The following set of exercises is given together with hints, solutions, and solution paths. They are designed such that you can first try to solve them and in case you need help, please, open the "hints" section. For checking your answer, please, open the "solution" section and for getting more details or checking your way of solving the exercise, please, open the "solution path" section.


Exercise 1: Finding doubling time for an investment

a) If Dato invests \(1000\) GEL at \(8\%\) annual interest, compounded continuously, how long does it take for his investment to be doubled? b) Would the doubling time of Dato's investment change if the principal were something other than \(1000\) GEL?

Hint (please, click on the "+" sign to read more) In general, a quantity \(Q(t) = Q_0 {\rm{e}}^{kt}\) (\(k > 0\)) doubles when \(t=d\), where \[ d \, \, = \, \, \frac{\ln(2)}{k} \, , \] \[ 2 Q_0 \, \, = \, \, Q_0 {\rm{e}}^{kd} \quad \Rightarrow \quad 2 \, \, = \, \, {\rm{e}}^{kt} \quad \Rightarrow \quad \ln(2) \, \, = \, \, kd \quad \Rightarrow \quad d \, \, = \, \, \frac{\ln(2)}{k} \, . \]

Solution (please, click on the "+" sign to read more) Doubling time is \(8.66\), when principal is \(1000\). This doubling time would not change if the principal were different from \(1000\).

Solution Path (please, click on the "+" sign to read more) a) With a principal of \(1000\) GEL, the balance after \(t\) years is \(B(t) = 1000 {\rm{e}}^{0.08t}\), so the investment doubles when \(B(t) = 2000\) GEL, that is, when \[ 2000 \, \, = \, \, 1000 {\rm{e}}^{0.08 t} \, \] Dividing by \(1000\) and taking the natural logarithm on each side of the equation, we get \[ 2 \, \, = \, \, {\rm{e}}^{0.08 t} \quad \Rightarrow \quad \ln(2) \, \, = \, \, 0.08 t \quad \Rightarrow \quad t \, \, = \, \, \tfrac{\ln(2)}{0.08} \, \, \approx \, \, 8.66 \quad \text{years} \, . \] b) If the principal had been \(P_0\) GEL instead of \(1000\) GEL, the doubling time would satisfy \[ 2 P_0 \, \, = \, \, P_0 {\rm{e}}^{0.08 t} \qquad \Longrightarrow \qquad 2 \, \, = \, \, {\rm{e}}^{0.08t} \] which is exactly the same equation we had with \(P_0 = 1000\) GEL, so once again, the doubling time is \(8.66\) years.

Exercise 2: Computing an interest rate

Anao has \(1500\) GEL to invest and wants it to grow to \(2000\) in \(5\) years. At what annual rate \(r\) compounded continuously must she invest her money to achieve her goal?

Hint (please, click on the "+" sign to read more) If interest is compounded continuously, future value is \[ B(t) \, \, = \, \, P {\rm{e}}^{rt} \, . \]

Solution (please, click on the "+" sign to read more) The annual interest rate is approximately \(5.75\%\).

Solution Path (please, click on the "+" sign to read more) If the interest rate is \(r\), the future value of \(1500\) in \(5\) years is given by \(1500 {\rm{e}}^{5 r}\). For this to equal \(2000\), we must have \[ 1500 {\rm{e}}^{5 r} \, \, = \, \, 2000 \quad \Longrightarrow \quad {\rm{e}}^{5r} \, \, = \, \, \tfrac{2000}{1500} \, \, = \, \, \tfrac{4}{3} \, . \] Taking natural logarithms on both sides of this equation, we get \[ \ln( {\rm{e}}^{5r} ) \, \, = \, \, \ln( \tfrac{4}{3} ) \quad \Longrightarrow \quad 5r \, \, = \, \, \ln( \tfrac{4}{3} ) \quad \Longrightarrow \quad r \, \, = \, \, \tfrac{1}{5} \ln( \tfrac{4}{3} ) \, \, \approx \, \, 0.0575 \, . \]

Exercise 3: Examining a Learning Model

The rate at which a postal clerk can sort mail is a function of the clerk's experience. Suppose the postmaster of a large city estimates that after \(t\) months on the job, the average clerk can sort \(Q(t) = 700 - 400 {\rm{e}}^{-0.5t}\) letters per hour: a) How many letters can a new employee sort per hour? b) How many letters can a clerk with 6 months' experience sort per hour? c) Approximately how many letters will the average clerk ultimately be able to sort per hour?

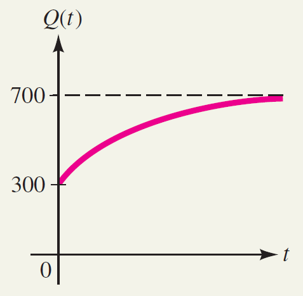
Hint (please, click on the "+" sign to read more) Use the graph and observe what happens then \(t\) increases.

Solution (please, click on the "+" sign to read more) a) \(300\) b) \(680\) c) The average clerk will ultimately be able to sort approximately \(700\) letters per hour.

Solution Path (please, click on the "+" sign to read more) a) The number of letters a new employee can sort per hour is \[ Q(0) \, \, = \, \, 700 - 400 {\rm{e}}^{0} \, \, = \, \, 300 \, . \] b) After \(6\) months, the average clerk can sort \begin{eqnarray} Q(6) & = & 700 - 400 {\rm{e}}^{-0.5 \cdot 6} \, \, = \, \, 700 - 400 {\rm{e}}^{-3} \\ & \approx & 680 \quad \text{letters per hour} \, . \end{eqnarray} c) As \(t\) increases without bound, \(Q(t)\) approaches \(700\). Hence, the average clerk will ultimately be able to sort approximately \(700\) letters per hour. The graph of the function \(Q(t)\) is sketched in the figure.

Exercise 4: Studying the progress of an epidemic

Public health records indicate that \(t\) weeks after the outbreak of a certain strain of influenza, approximately \(Q(t) = \frac{20}{1 + 19 {\rm{e}}^{-1.2 t}}\) thousand people had caught the disease. a) How many people had the disease when it broke out? How many had it \(2\) weeks later? b) At what time does the rate of infection begin to decline? c) If the trend continues, approximately how many people will eventually contract the disease?

Hint (please, click on the "+" sign to read more)

Solution (please, click on the "+" sign to read more) a) \(1000\) people initially had the disease, and about \(7343\) by the second week. b) Epidemic begins to fade about \(2.5\) weeks after it starts c) \(20 000\) people will eventually contract the disease.

Solution Path (please, click on the "+" sign to read more) a) Since \(Q(0) = \frac{20}{1+19} = 1\), it follows that \(1000\) people initially had the disease. When \(t=2\), \[ Q(2) \, \, = \, \, \frac{20}{1 + 19 {\rm{e}}^{-1.2 \cdot 2}} \, \, \approx \, \, 7.343 \, , \] so about \(7343\) had contracted the disease by the second week. b) The rate of infection begins to decline at the inflection point on the graph of \(Q(t)\). By comparing the given formula with the logistic formula \(Q(t) = \frac{B}{1 + A {\rm{e}}^{-Bkt}}\), we find that \(B = 20\), \(A = 19\), and \(Bk = 1.2\). Thus, the inflection point occurs when \[ t \, \, = \, \, \frac{\ln(A)}{BK} \, \, = \, \, \frac{\ln(19)}{1.2} \, \, \approx \, \, 2.454 \, , \] so the epidemic begins to fade about \(2.5\) weeks after it starts. c) Since \(Q(t)\) approaches \(20\) as \(t\) increases without bound, it follows that approximately \(20 000\) people will eventually contract the disease.