return to the main page "Calculus I for Management"
return to the section "Exponential Functions & Marginal Analysis"
Worked-Out Exercises: Marginal Analysis
& Related Rates
The following set of exercises is given together with hints, solutions, and solution paths. They are designed such that
you can first try to solve them and in case you need help, please, open the "hints" section. For checking your
answer, please, open the "solution" section and for getting more details or checking your way of solving the
exercise, please, open the "solution path" section.
|
|
|
Exercise 1: marginal cost and marginal revenue |
| |
|
A manufacturer estimates that when \(x\) units of a particular commodity are produced,
the total cost will be
\[
C(x) \, \, = \, \, \tfrac{1}{8} x^2 + 3x + 98 \quad \text{[GEL]} \, ,
\]
and furthermore, that all \(x\) units will be sold when the price is
\[
p(x) \, \, = \, \, \tfrac{1}{3} \left( 75 - x \right) \quad \text{[GEL per unit]} \, .
\]
a) Find the marginal cost and the marginal revenue.
b) Use marginal cost to estimate the cost of producing the \(37\)th unit. What is the
actual cost of producing the \(37\)th unit?
c) Use marginal revenue to estimate the revenue derived from the sale of the \(37\)th
unit. What is the actual revenue derived from the sale of the \(37\)th unit?
|
|
 Hint
(please, click on the "+" sign to read more)
If \(C(x)\) is the total cost of producing \(x\) units of a commodity, then the marginal cost of producing \(x_0\) units is the derivative \(C'(x_0)\). additional cost \(C(x_0+1)-C(x_0)\)
incurred when the level of production is increased from \(x_0\) to \(x_0+1\).
Same discussion applies to revenue.
|
|
Solution
(please, click on the "+" sign to read more)
a) The marginal cost is \(C'(x) = \tfrac{1}{4} x + 3\) and marginal revenue equals R'(x) = \( 25 - \tfrac{2}{3} x\)
b) The actual cost of producing the \(37\)th unit is \(C(37) - C(36) = 380.125 - 368 = 12.125\) GEL
c) The actual revenue obtained from the sale of the \(37\)th unit is \(R(37) - R(36) = 468.67 - 468 = 0.67\)
|
|
Solution Path
(please, click on the "+" sign to read more)
a) The marginal cost is \(C'(x) = \tfrac{1}{4} x + 3\). Since \(x\) units of the commodity are sold
at a price of \(p(x) = \tfrac{1}{3}(75-x)\) GEL per unit, the total revenue is
\begin{eqnarray*}
R(x) & = & (\text{number of units sold})(\text{price per unit}) \, \, = \, \, x \cdot p(x)
& = &
25x - \tfrac{1}{3} x^2
\end{eqnarray*}
The marginal revenue is
\[
R'(x) \, \, = \, \, 25 - \tfrac{2}{3} x
\]
b) The cost of producing the \(37\)th unit is the change in cost as \(x\) increases from
\(36\) to \(37\) and can be estimated by the marginal cost when producing \(36\) units:
\[
C'(x) \, \, = \, \, \tfrac{1}{4} \cdot 36 + 3 \, \, = \, \, 12 \quad [GEL]
\]
The actual cost of producing the \(37\)th unit is \(C(37) - C(36) = 380.125 - 368 = 12.125\) GEL
which is reasonably well approximated by the marginal cost \(C'(36)=12\) GEL.
c) The revenue obtained from the sale of the \(37\)th unit is approximated by the marginal
revenue at \(x=36\):
\[
R'(x) \, \, = \, \, 25 - \tfrac{2}{3} \cdot 36 \, \, = \, \, 1 \quad [GEL]
\]
The actual revenue obtained from the sale of the \(37\)th unit is
\[
R(37) - R(36) \, \, = \, \, 468.67 - 468 \, \, = \, \, 0.67
\]
that is, \(0.67\) GEL, which is approximately the same as the marginal revenue
\(R'(36)=1\) GEL.
|
|
Exercise 2: Estimating change in cost using a derivative |
| |
|
Suppose the total cost of manufacturing q hundred units of a certain commodity is \(C\)
thousand GEL where \(C(q)=3q^2+5q+10\). If the current level of production is
\(4000\) units, estimate how the total cost will change if \(4050\) units are produced.
|
|
Hint
(please, click on the "+" sign to read more)
if \(\Delta f = f(x_0 + \Delta x) - f(x_0)\), then
\[
\Delta f \, \, \approx \, \, f'(x_0) \cdot \Delta x \, .
\]
|
|
Solution
(please, click on the "+" sign to read more)
Total cost will change by
\[
\Delta C \, \, \approx \, \, C'(40) \cdot 0.5 \, \, = \, \, 245 \cdot 0.5 \, \, = \, \, 122.5 \, .
\]
|
|
Solution Path
(please, click on the "+" sign to read more)
In this problem, the current level of production is \(q=40\) (i.e. \(4000\) units) and the change
in production is \(\Delta q = 0.5\) (an additional \(50\) units). By the approximation formula,
the corresponding change in cost is
\[
\Delta C \, \, = \, \, C(40.5) - C(40) \, \, \approx \, \, C'(40) \cdot \Delta q \, \, = \, \, C'(40) \cdot 0.5
\]
Since \(C'(q) = 6q + 5\) and \(C'(40) = 6 \cdot 40 + 5 = 245\) it follows that
\[
\Delta C \, \, \approx \, \, C'(40) \cdot 0.5 \, \, = \, \, 245 \cdot 0.5 \, \, = \, \, 122.50 \, .
\]
|
|
Exercise 3: Related Rates |
| |
|
Air is being pumped into a spherical balloon so that its volume increases
at a rate of \(100\) \(cm^3/s\). How fast is the radius of the balloon increasing when the diameter
is \(50\) \(cm\)?
|
|
Hint
(please, click on the "+" sign to read more)
The key thing to remember is that rates of change are derivatives. In this problem, the
volume and the radius are both functions of the time \(t\). The rate of increase of the volume
with respect to time is the derivative \(\frac{\textrm{d} \, V}{\textrm{d} \, t}\), and the rate of increase of the radius is \(\frac{\textrm{d} \, r}{\textrm{d} \, t}\).
|
|
Solution
(please, click on the "+" sign to read more)
The radius of the balloon is increasing at the rate of \(1/(25 \pi) \approx 0.0127\) \(cm/s\).
|
|
Solution Path
(please, click on the "+" sign to read more)
We start by identifying two things:
First, given information: the rate of increase of the volume of air is \(100\) \(cm^3/s\), and
second, unknown: the rate of increase of the radius when the diameter is \(50\) \(cm\).
In order to express these quantities mathematically, we introduce some suggestive
notation:
\[
\text{Let \(V\) be the volume of the balloon and let \(r\) be its radius.}
\]
The key thing to remember is that rates of change are derivatives. In this problem, the
volume and the radius are both functions of the time \(t\). The rate of increase of the volume
with respect to time is the derivative \(\frac{\textrm{d} \, V}{\textrm{d} \, t}\), and the rate of increase of the radius is \(\frac{\textrm{d} \, r}{\textrm{d} \, t}\).
We can therefore restate the given and the unknown as follows:
Given: \(\frac{\textrm{d} \, V}{\textrm{d} \, t} = 100\) \(cm^3/s\)
Unknown: \(\frac{\textrm{d} \, r}{\textrm{d} \, t}\) when \(r = 25\) \(cm^3/s\)
In order to connect \(\frac{\textrm{d} \, V}{\textrm{d} \, t}\) and \(\frac{\textrm{d} \, r}{\textrm{d} \, t}\), we first relate \(V\) and \(r\) by the formula for the
volume of a sphere:
\[
V \, \, = \, \, \tfrac{4}{3} \, \pi \, r^3 \, .
\]
In order to use the given information, we differentiate each side of this equation with
respect to \(t\).
To differentiate the right side, we need to use the Chain Rule:
\[
\frac{\textrm{d} \, V}{\textrm{d} \, t} \, \, = \, \, \frac{\textrm{d} \, V}{\textrm{d} \, r} \frac{\textrm{d} \, r}{\textrm{d} \, t}
\, \, = \, \, 4 \pi r^2 \frac{\textrm{d} \, r}{\textrm{d} \, t} \, .
\]
Now we solve for the unknown quantity:
\[
\frac{\textrm{d} \, r}{\textrm{d} \, t} \, \, = \, \, \frac{1}{4 \pi r^2} \, \frac{\textrm{d} \, V}{\textrm{d} \, t} \,.
\]
If we put \(r = 25\) and \(\frac{\textrm{d} \, V}{\textrm{d} \, t} = 100\) in this equation, we obtain
\[
\frac{\textrm{d} \, r}{\textrm{d} \, t} \, \, = \, \, \frac{1}{4 \pi 25^2} \, 100 \, \, = \, \, \frac{1}{25 \pi} \, .
\]
The radius of the balloon is increasing at the rate of \(1/(25 \pi) \approx 0.0127\) \(cm/s\).
|
|
Exercise 4: Related Rates |
| |
|
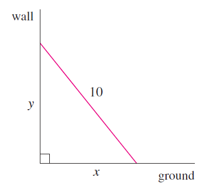
A ladder \(10\) meter long rests against a vertical wall. If the bottom of the ladder
slides away from the wall at a rate of \(1\) meter, how fast is the top of the ladder sliding
down the wall when the bottom of the ladder is \(6\) meter from the wall?
|
|
Hint
(please, click on the "+" sign to read more)
\[
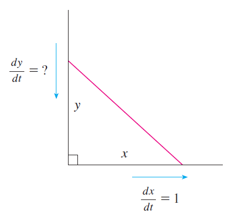\frac{\textrm{d} \, y}{\textrm{d} \, t} \, \, = \, \, - \frac{x}{y} \, \frac{\textrm{d} \, x}{\textrm{d} \, t}
\]
|
|
Solution
(please, click on the "+" sign to read more)
The top of the ladder is sliding down the wall at a rate of \(34\) \(m\).
|
|
Solution Path
(please, click on the "+" sign to read more)
We first draw a diagram and label it as in the figure. Let \(x\) meter be the distance
from the bottom of the ladder to the wall and \(y\) meter the distance from the top of
the ladder to the ground.
Note that \(x\) and \(y\) are both functions of \(t\) (time, measured in
seconds).
We are given that \(\frac{\textrm{d} \, x}{\textrm{d} \, t} = 1\) \(m/s\) and we are asked to find \(\frac{\textrm{d} \, y}{\textrm{d} \, t}\) when \(x = 6\) \(m\)
In this problem, the relationship between x and y is given by the Pythagorean
Theorem:
\[
x^2 \, + \, y^2 \, \, = \, \, 100 \, .
\]
Differentiating each side with respect to \(t\) using the Chain Rule, we have
\[
2x \, \frac{\textrm{d} \, x}{\textrm{d} \, t} \, + \, 2y \, \frac{\textrm{d} \, y}{\textrm{d} \, t} \, \, = \, \, 0 \, ,
\]
and solving this equation for the desired rate, we obtain
\[
\frac{\textrm{d} \, y}{\textrm{d} \, t} \, \, = \, \, - \frac{x}{y} \, \frac{\textrm{d} \, x}{\textrm{d} \, t} \, .
\]
When \(x = 6\), the Pythagorean Theorem gives \(y = 8\) and so, substituting these values
and \(\frac{\textrm{d} \, x}{\textrm{d} \, t} = 1\), we have
\[
\frac{\textrm{d} \, y}{\textrm{d} \, t} \, \, = \, \, -\frac{6}{8} \cdot 1 \, \, = \, \, -\frac{3}{4} \, \, \, [m/s] \, .
\]
The fact that \(\frac{\textrm{d} \, y}{\textrm{d} \, t}\) is negative means that the distance from the top of the ladder to
the ground is decreasing at a rate of \(34\) \(m\). In other words, the top of the ladder is sliding
down the wall at a rate of \(34\) \(m\).
|
|
|
Copyright Kutaisi International University — All Rights Reserved — Last Modified: 12/ 10/ 2022
|
|
| |