Mathematics for Management -- Supplementary Electronic Materials

return to the main page "Calculus I for Management"
return to the section "Curves & Optimization"

Worked-Out Exercises: Curve Sketching

The following set of exercises is given together with hints, solutions, and solution paths. They are designed such that you can first try to solve them and in case you need help, please, open the "hints" section. For checking your answer, please, open the "solution" section and for getting more details or checking your way of solving the exercise, please, open the "solution path" section.


Exercise 1: Applying the guidelines of curve sketching

Use the guidelines to sketch the curve \[ y \, \, = \, \, f(x) \, \, = \, \, \frac{\cos(x)}{2 + \sin(x)} \, . \]

Hint (please, click on the "+" sign to read more) Remember that in order to sketch curves you'll need to find the domain of a function, interception points, symmetry, Asymptotes, intervals of increase and decrease, local maximum and minimum, concavity and inflection points and only then graph the function itself.

Solution (please, click on the "+" sign to read more)

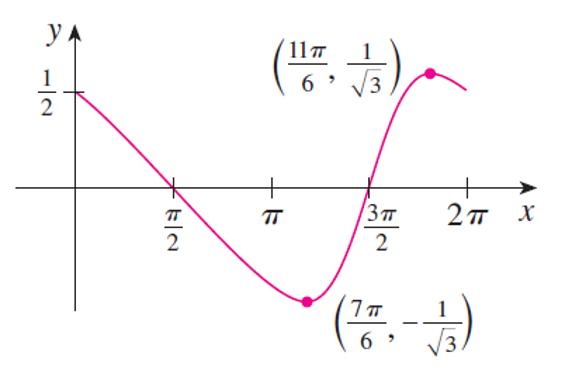
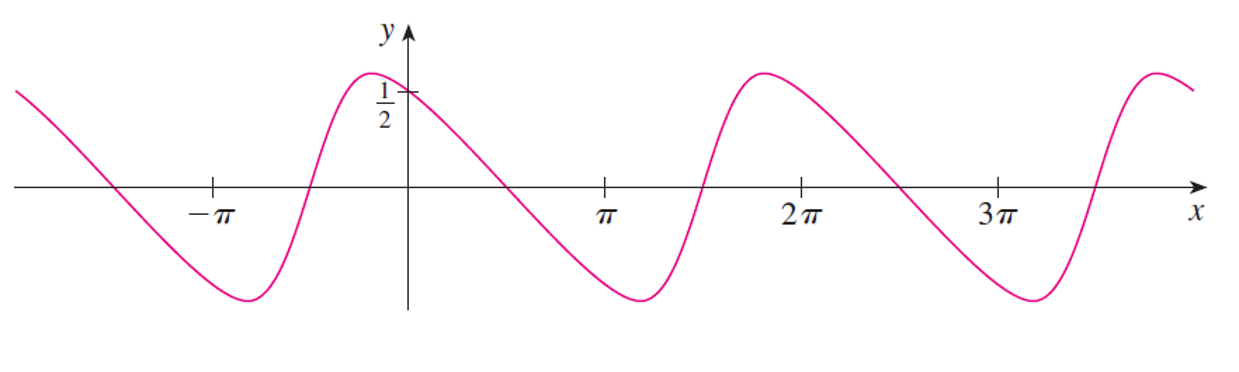
Solution Path (please, click on the "+" sign to read more) \({\bf{A)}}\) The domain is \(D \, = \, \mathbb{R} \, = \, (-\infty, \infty)\) \({\bf{B)}}\) The \(x\)-intercepts occur when \(\cos(x) = 0\), i.e., \(x = \tfrac{1}{2} \pi + n \pi\), where \(n \in \mathbb{Z}\) is an integer. The \(y\)-intercept is \(f(0) = \tfrac{1}{2}\). \({\bf{C)}}\) \(f\) is neither even nor odd, but \(f(x + 2 \pi) = f(x)\) for all \(x\) and so \(f\) is periodic and has period \(2 \pi\). Thus, in what follows, we need to consider only \(0 \leq x \leq 2 \pi\) and then extend the curve by translation in part \({\bf{H)}}\). \({\bf{D)}}\) There are no asymptotes. \({\bf{E)}}\) The first derivative of \(f\) is \[ f'(x) \, \, = \, \, \frac{\left(2 + \sin(x) \right) \cdot \left( -\sin(x) \right) - \cos(x) \cdot \cos(x)}{\left( 2 + \sin(x) \right)^2} \, \, = \, \, -\frac{2 \sin(x) + 1}{\left( 2 + \sin(x) \right)^2} \] The denominator is always positive, so \(\begin{eqnarray} f'(x) \, > \, 0 & \Longleftrightarrow & 2 \sin(x) + 1 \, < \, 0 \quad \Longleftrightarrow \quad 2 \sin(x) \, < \, -\tfrac{1}{2}\\[1mm] & \Longleftrightarrow &\tfrac{7}{6} \pi \, < \, x \, < \, \tfrac{11}{6} \pi \, . \end{eqnarray}\) Hence, \(f\) is increasing on \((\tfrac{7}{6} \pi, \tfrac{11}{6} \pi)\) and decreasing on \((0, \tfrac{7}{6} \pi)\) and \((\tfrac{11}{6} \pi, 2 \pi)\). \({\bf{F)}}\) From part \({\bf{E)}}\) and the first derivative test, we have that the local minimum value is \(f(\tfrac{7}{6} \pi) = -\frac{1}{\sqrt{3}}\) and the local maximum value is \(f(\tfrac{11}{6} \pi) = \frac{1}{\sqrt{3}}\). \({\bf{G)}}\) If we use the quotient rule again and simplify, we get \[ f''(x) \, \, = \, \, -\frac{2 \, \cos(x) \, \left( 1 - \sin(x) \right)}{\left( 2 + \sin(x) \right)^3} \] Because \(\left( 2 + \sin(x) \right)^3 > 0\) and \(1 - \sin(x) \geq 0\) for all \(x\), we have that \[ f''(x) \, \, > \, \, 0 \quad \Longleftrightarrow \quad \cos(x) \, \, > \, \, 0 \quad \Longleftrightarrow \quad \tfrac{1}{2} \pi \, \, < \, \, x \, \, < \, \, \tfrac{3}{2} \pi \, . \] So \(f\) is concave upward on \((\tfrac{1}{2} \pi, \tfrac{3}{2} \pi\)) and concave downward on \((0, \tfrac{1}{2})\) and \((\pi, \tfrac{3}{2} \pi, 2 \pi\)). The inflection points are \((\tfrac{1}{2} \pi, 0)\) and \((\tfrac{3}{2} \pi, 0)\). \({\bf{H)}}\) We first sketch the graph of the function restricted to one period length \(0 \leq x \leq 2 \pi\). Then we extend it, using periodicity, to complete the graph:

Exercise 2: Solving optimization problems

A farmer has \(2400\) meter of fencing and wants to fence off a rectangular field that borders a straight river. He needs no fence along the river. What are the dimensions of the field that has the largest area?

Hint (please, click on the "+" sign to read more) Recall, that the maximum value of area must occur either at the critical number or at an endpoint of the interval.

Solution (please, click on the "+" sign to read more) Field should be \(600\) meter deep and \(1200\) meter wide.

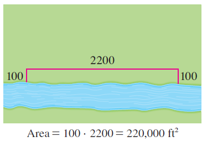
Solution Path (please, click on the "+" sign to read more) In order to get a feeling for what is happening in this problem, let's experiment with some specific cases. The figure (not to scale) shows three possible ways of laying out the \(2400\) meter of fencing. We see that when we try shallow, wide fields or deep, narrow fields, we get relatively small areas. It seems plausible that there is some intermediate configuration that produces the largest area. 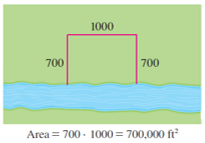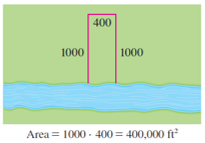The figure illustrates the general case. We wish to maximize the area \(A\) of the rectangle. Let \(x\) and \(y\) be the depth and width of the rectangle (in meter). Then we express \(A\) in terms of \(x\) and \(y\): \[ A \, \, = \, \, x \cdot y \, . 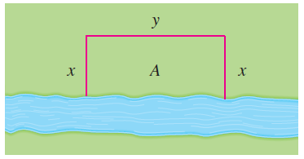\] We want to express \(A\) as a function of just one variable, so we eliminate \(y\) by expressing it in terms of \(x\). To do this we use the given information that the total length of the fencing is \(2400\) meter. Thus \[ 2x \, + \, y \, \, = \, \, 2400 \, . \] From this equation we have \(y = 2400 - 2x\), which gives \[ A \, \, = \, \, x \cdot y \, \, = \, \, x \, \left( 2400 - 2 x \right) \, \, = \, \, 2400 \, x \, - \, 2 \, x^2 \, . \] Note that the largest \(x\) can be is \(1200\) (this uses all the fence for the depth and none for the width) and \(x\) can't be negative, so the function that we wish to maximize is \[ A(x) \, \, = \, \, 2400 \, x \, - \, 2 \, x^2 \, , \qquad 0 \, \, \leq \, \, x \, \, \leq \, \, 1200 \, . \] The derivative is \(A'(x) = 2400 - 4 x\), so to find the critical numbers we solve the equation \[ 2400 \, - \, 4 \, x \, \, = \, \, 0 \qquad \Longleftrightarrow \qquad x \, \, = \, \, 600 \, . \] The maximum value of \(A\) must occur either at this critical number or at an endpoint of the interval. Since \(A(0) = 0\), \(A(600) = 720000\), and \(A(1200) = 0\), we get the maximum value as \(A(600) = 720000\). The corresponding \(y\)-value is \(y = 2400 - 2 \cdot 600 = 1200\); so the rectangular field should be \(600\) meter deep and \(1200\) meter wide.

Exercise 3: Solving optimization problems

A cylindrical can is to be made to hold \(1\) liter of oil. Find the dimensions that will minimize the cost of the metal to manufacture the can.

Hint (please, click on the "+" sign to read more) At first, write the function of area in terms of \(r\) and then find the minimum of it using the differentiation.

Solution (please, click on the "+" sign to read more) Radius is equal to \(\sqrt[3]{500/ \pi}\) \(cm\) and the height is \(2 \sqrt[3]{500/ \pi}\) \(cm\)

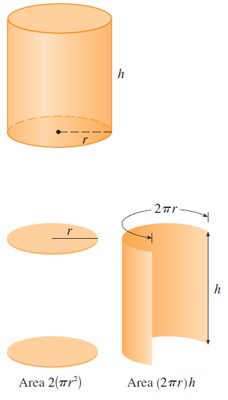
Solution Path (please, click on the "+" sign to read more) Draw the diagram, where \(r\) is the radius and \(h\) the height (both in centimeters). In order to minimize the cost of the metal, we minimize the total surface area of the cylinder (top, bottom, and sides). From the figure we see that the sides are made from a rectangular sheet with dimensions \(2 \pi r^2\) and \(h\). So the surface area is \[ A \, \, = \, \, 2 \, \pi \, r^2 \, + \, 2 \, \pi \, r \, h \, . \] We would like to express \(A\) in terms of one variable, \(r\). To eliminate \(h\) we use the fact that the volume is given as \(1\) liter, which is equivalent to \(1000\) \(cm^3\). Thus \[ \pi \, r^2 \, h \, \, = \, \, 1000 \qquad \Longleftrightarrow \qquad h \, \, = \, \, \frac{1000}{\pi \, r^2} \] Substitution of this into the expression for \(A\) gives \[ A \, \, = \, \, 2 \, \pi \, r^2 \, + \, 2 \, \pi \, r \, \left( \frac{1000}{\pi \, r^2} \right) \, \, = \, \, 2 \, \pi \, r^2 \, + \, \frac{2000}{r} \, . \] We know \(r\) must be positive, and there are no limitations on how large \(r\) can be. Therefore the function that we want to minimize is \[ A(r) \, \, = \, \, 2 \, \pi \, r^2 \, + \, \frac{2000}{r} \, , \qquad r \, \, > \, \, 0 \, . \] To find the critical numbers, we differentiate: \[ A'(r) \, \, = \, \, 4 \, \pi \, r \, - \, \frac{2000}{r^2} \, \, = \, \, \frac{4 \, \left( \pi r^3 - 500 \right)}{r^2} \, . \] Then \(A'(r) = 0\) when \(\pi r^3 = 500\), so the only critical number is \(r = \sqrt[3]{500/ \pi}\). Due to \(A'(r) < 0\) for \(r < \sqrt[3]{500/ \pi}\) and \(A'(r) > 0\) for \(r > \sqrt[3]{500/ \pi}\), we have that \(A\) is decreasing for all \(r\) to the left of the critical number and increasing for all \(r\) to the right. Thus \(r = \sqrt[3]{500/ \pi}\) must give rise to an absolute minimum. The value of \(h\) corresponding to \(r = \sqrt[3]{500/ \pi}\) is \[ h \, \, = \, \, \frac{1000}{\pi \, r^2} \, \, = \, \, \frac{1000}{\pi \, \left( 500/ \pi \right)^{2/3}} \, \, = \, \, 2 \sqrt[3]{500/ \pi} \, \, = \, \, 2 r \] Thus, to minimize the cost of the can, the radius should be \(r = \sqrt[3]{500/ \pi}\) \(cm\) and the height should be equal to twice the radius, namely, the diameter. \({\bf{Alternative}}\) \({\bf{solution}}\) \({\bf{using}}\) \({\bf{implicit}}\) \({\bf{differentiation}}\) An alternative method for solving optimization problems is to use \({\bf{implicit}}\) \({\bf{differentiation}}\). Let's look at the previous example with the optimization of a can again to illustrate the method. We work with the same equations \[ A \, \, = \, \, 2 \, \pi \, r^2 \, + \, 2 \, \pi \, r \, h \, , \qquad \pi \, r^2 \, h \, \, = \, \, 1000 \] but instead of eliminating \(h\), we differentiate both equations implicitly with respect to \(r\): \[ A' \, \, = \, \, 4 \, \pi \, r \, + \, 2 \, \pi \, r \, h' \, + \, 2 \, \pi \, h \, , \qquad \pi \, r^2 \, h' \, + \, 2 \, \pi \, r \, h \, \, = \, \, 0 \] The minimum occurs at a critical number, so we set \(A' = 0\), simplify, and arrive at the equations \[ 2 \, r \, + \, r \, h' \, + \, h \, \, = \, \, 0 \, , \qquad r \, h' \, + \, 2 \, h \, \, = \, \, 0 \] and subtraction gives \(2 r - h = 0\), or \(h = 2r\).

Exercise 4: Estimating additional revenue using marginal revenue

A manufacturer determines that \(x\) units of a particular item will be sold when the price is \(p(x) = 112 - x \ln(\sqrt{x})\) hundred GEL per unit. \({\bf{a)}}\) Find the revenue and marginal revenue as functions of the number of units produced and sold \({\bf{b)}}\) Use marginal analysis to estimate the revenue obtained from producing the \(12\)th unit. What is the actual revenue obtained from producing the \(12\)th unit?

Hint (please, click on the "+" sign to read more) Function of a marginal revenue is a derivative of revenue function.

Solution (please, click on the "+" sign to read more) \({\bf{a)}}\) \(\, \, 112 - \tfrac{1}{2} x - x \ln(x) \, . \) \({\bf{b)}}\) \(78.16\)

Solution Path (please, click on the "+" sign to read more) \({\bf{a)}}\) The revenue is \[ R(x) \, \, = \, \ x \cdot p(x) = x \cdot \left( 112 - x \ln(x) \right) \, \, = \, \, 112x - \tfrac{1}{2} x^2 \ln(x) \] hundred GEL, and the marginal revenue is \[ R'(x) \, \, = \, \, 112 - \tfrac{1}{2} \left( x^2 \cdot \tfrac{1}{x} + 2x \cdot \ln(x) \right) \, \, = \, \, 112 - \tfrac{1}{2} x - x \ln(x) \, . \] \({\bf{b)}}\) The additional revenue obtained from producing the \(12\)th unit is estimated by the marginal revenue generated by the \(11\)th unit, that is, by \[ R'(11) \, \, = \, \, 112 - \tfrac{11}{2} - 11 \ln(11) \, \, \approx \, \, 80.12 \, . \] So marginal analysis suggests that the manufacturer will receive approximately \(80.12\) hundred GEL in additional revenue by producing the \(12\)th unit. To check the accuracy of this estimate, the actual additional revenue is \(\begin{eqnarray} R(12) - R(11) & = & \left( 112 \cdot 12 - \tfrac{12^2}{2} \ln(12) \right) - \left( 112 \cdot 11 - \tfrac{11^2}{2} \ln(11) \right)\\[1mm] & \approx & 1165.09 - 1086.93 \, \, = \, \, 78.16 \end{eqnarray}\) hundred GEL.

Exercise 5: Studying elasticity of demand

Edgar is the manager of a manufacturing firm. He determines that \(D(p) = 5 000 {\rm{e}}^{-0.02p}\) units of the company's product will be demanded (sold) when the price is \(p\) dollars per unit. \({\bf{a)}}\) Find the elasticity of demand for this commodity. For what values of \(p\) is the demand elastic, inelastic, and of unit elasticity? \({\bf{b)}}\) If Edgar decides to increase the price \(3\%\) from the current level of \(40\) GEL, what change in demand should he expect? \({\bf{c)}}\) Find the revenue \(R(p)\) obtained by selling \(q=D(p)\) units at \(p\) GEL per unit. For what value of \(p\) is the revenue maximized?

Hint (please, click on the "+" sign to read more) Formula of elacticity of demand is \(E(p) = -\frac{p}{q} \frac{\textrm{d} q}{\textrm{d} p} \, \,\)

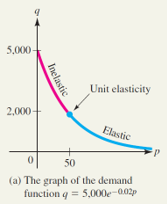
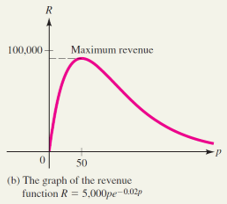
Solution (please, click on the "+" sign to read more) \({\bf{a)}}\) \( E(p) = 0.02p\) demand is of unit elasticity when \(E(p) = 0.02p = 1\), that is, when \(p=50\), demand is elastic when \(E(p) = 0.02p > 1\), or \(p > 50\), and demand is inelastic when \(E(p) = 0.02p < 1\), or \(p < 50\). \({\bf{b)}}\) decrease in demand from \(2247\) to \(2193\) units. \({\bf{c)}}\) When \(p=50\).

Solution Path (please, click on the "+" sign to read more) \({\bf{a)}}\) According to the formula previously derived, the elasticity of demand is given by \(\begin{eqnarray} E(p) & = & -\frac{p}{q} \frac{\textrm{d} q}{\textrm{d} p} \, \, = \, \, -\frac{p}{5000 {\rm{e}}^{-0.02 p}} \cdot \left( 5000 {\rm{e}}^{-0.02 p} \cdot (-0.02) \right) & = & 0.02 p \end{eqnarray}\) so demand is of unit elasticity when \(E(p) = 0.02p = 1\), that is, when \(p=50\), demand is elastic when \(E(p) = 0.02p > 1\), or \(p > 50\), and demand is inelastic when \(E(p) = 0.02p < 1\), or \(p < 50\). The graph of the demand function, showing levels of elasticity, is displayed in the figure. \({\bf{b)}}\) When \(p = 40\), the demand is \[ q(40) \, \, = \, \, 5000 {\rm{e}}^{-0.02 \cdot 40} \, \, \approx \, \, 2247 \quad \text{units} \] and the elasticity of demand is \[ E(40) \, \, = \, \, 0.02 \cdot 40 \, \, = \, \, 0.8 \, . \] Thus, an increase of \(1\%\) in price from \(p = 40\) GEL will result in a decrease in the quantity demanded by approximately \(0.8\%\). Consequently, an increase of \(3\%\) in price, from \(40\) GEL to \(41.20\) GEL, results in a decrease in demand of approximately \(2 247 \cdot 3 \cdot 0.008 = 54\) units, from \(2247\) to \(2193\) units. \({\bf{c)}}\) The revenue function is \[ R(p) \, \, = \, \, p \cdot q \, \, = \, \, 5000 p {\rm{e}}^{-0.02p} \] for \(p \geq 0\) (only nonnegative prices have economic meaning), with derivative \[ R'(p) \, \, = \, \, 5000 \left( -0.02 p {\rm{e}}^{-0.02p} + {\rm{e}}^{-0.02p} \right) \, \, = \, \, 5000 \left( 1 - 0.02 p \right) {\rm{e}}^{-0.02p} \, . \] Since \({\rm{e}}^{-0.02p}\) is always positive, \(R'(p)=0\) if and only if \[ 1 - 0.02 p \, \, = \, \, 0 \qquad \text{or} \qquad p \, \, = \, \, \tfrac{1}{0.02} \, \, = \, \, 50 \, . \] To verify that \(p=50\) actually gives the absolute maximum, note that \[ R''(p) \, \, = \, \, 5000 \left( 0.0004p - 0.04 \right) {\rm{e}}^{-0.02p} \quad \Longrightarrow \quad R''(50) \, \, \approx \, \, -37 \, \, < \, \, 0 \, . \] Thus, the second derivative test tells you that the absolute maximum of \(R(p)\) does indeed occur when \(p=50\).