Mathematics for Management -- Supplementary Electronic Materials

return to the main page "Calculus I for Management"
return to the page "The Fundamental Theorem of Calculus"

Worked-Out Exercises: Integration

The following set of exercises is given together with hints, solutions, and solution paths. They are designed such that you can first try to solve them and in case you need help, please, open the "hints" section. For checking your answer, please, open the "solution" section and for getting more details or checking your way of solving the exercise, please, open the "solution path" section.


Exercise 1: Finding indefinite integrals

Find the general indefinite integral. ${\displaystyle{ \int \frac{1 + \sqrt{x} + x}{x} \textrm{d} x }}$ ${\displaystyle{ \int \left( \sin(x) + \sinh(x) \right) \textrm{d} x }}$ ${\displaystyle{ \int \left( x^2 + 1 + \frac{1}{x^2 + 1} \right) \textrm{d} x }}$ ${\displaystyle{ \int \frac{\sin(2x)}{\sin(x)} \textrm{d} x }}$

Hint (please, click on the "+" sign to read more) Try to integrate parts of the equation one by one first.

Solution (please, click on the "+" sign to read more) $ln\|x\| + 2 x^{1/2} + x + C$ $-\cos(x) + \cosh(x) + C$ $x^3 + x + \arctan(x) + C$ $2 \sin(x) + C$

Solution Path (please, click on the "+" sign to read more) \begin{eqnarray} \int \frac{1 + \sqrt{x} + x}{x} \textrm{d} x & = & \int \left( x^{-1} + x^{-1/2} + 1 \right) \textrm{d} x \, \, = \, \, \ln\|x\| + 2 x^{1/2} + x + C \end{eqnarray} \begin{eqnarray} \int \left( \sin(x) + \sinh(x) \right) \textrm{d} x & = & -\cos(x) + \cosh(x) + C \end{eqnarray} \begin{eqnarray} \int \left( x^2 + 1 + \frac{1}{x^2 + 1} \right) \textrm{d} x & = & \tfrac{1}{3} x^3 + x + \arctan(x) + C \end{eqnarray} \begin{eqnarray} \int \, \frac{\sin(2x)}{\sin(x)} \, \textrm{d} x & = & \int \, \frac{2 \sin(x) \cos(x)}{\sin(x)} \, \textrm{d} x \, \, = \, \, \int \, 2 \cos(x) \, \textrm{d} x \, \, = \, \, 2 \sin(x) + C \end{eqnarray}

Exercise 2: Finding a function from its slope function

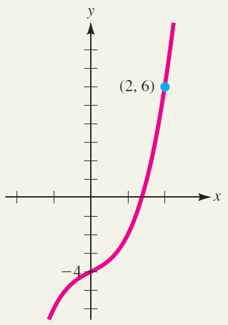
Find the function $f(x)$ whose tangent has slope $3 x^2 + 1$ for each value of $x$ and whose graph passes through the point $(2,6)$.

Hint (please, click on the "+" sign to read more) Remember that the slope of the tangent at each point $(x,f(x))$ is derivative $f'(x)$

Solution (please, click on the "+" sign to read more) $f(x) = x^3 + x - 4$

Solution Path (please, click on the "+" sign to read more) The slope of the tangent at each point $(x,f(x))$ is the derivative $f'(x)$. Thus, $f'(x) = 3 x^2 + 1$ and so $f(x)$ is the antiderivative $$ f(x) \, \, = \, \, \int \, f'(x) \, \textrm{d} x \, \, = \, \, \int \left( 3 x^2 + 1 \right) \textrm{d} x \, \, = \, \, x^3 + x + C \, . $$ To find $C$, use the fact that the graph of $f(x)$ passes through $(2,6)$. That is, substitute $x = 2$ and $f(2)=6$ into the equation for $f(x)$ and solve for $C$ to get $$ 6 \, \, = \, \, 2^3 + 2 + C \quad \Longrightarrow \quad C \, \, = \, \, -4 \, . $$ Thus, the desired function is $f(x) = x^3 + x - 4$.

Exercise 3: Antiderivatives

A particle moves in a straight line and has acceleration given by $a(t) = 6t +4$. Its initial velocity is $v(0) = -6$ $cm/s$ and its initial displacement is $s(0) = 9$ $cm$. Find its position function $s(t)$.

Hint (please, click on the "+" sign to read more) $v'(t) = a(t)$; $v(0) = 0$; $v(t) = s'(t)$

Solution (please, click on the "+" sign to read more) $$ s(t) \, \, = \, \, t^3 \, + \, 2 t^2 \, - \, 6t \, + \, 9 \, . $$

Solution Path (please, click on the "+" sign to read more) Since $v'(t) = a(t) = 6t + 4$, antidifferentiation gives $$ v(t) \, \, = \, \, 6 \cdot \frac{1}{2} t^2 \, + \, 4 t \, + \, C \, \, = \, \, 3 t^2 \, + \, 4t \, + \, C \, . $$ Note that $v(0) = C$. But we are given that $v(0) = -6$, so $C = -6$ and $$ v(t) \, \, = \, \, 3 t^2 \, + \, 4 t \, - \, 6 $$ Since $v(t) = s'(t)$, the position $s$ is the antiderivative of $v$: \begin{eqnarray} s(t) & = & \int \, v(t) \, \textrm{d} t \, \, = \, \, \int \left( 3 t^2 + 4 t - 6 \right) \textrm{d} t \\[2mm] & = & 3 \cdot \tfrac{1}{3} t^3 \, + \, 4 \cdot \tfrac{1}{2} t^2 \, - \, 6 t \, + \, D \, \, = \, \, t^3 \, + \, 2 t^2 \, - \, 6t \, + \, D \, . \end{eqnarray} This gives $s(0) = D$. We are given that $s(0) = 9$, so $D = 9$ and the required position function is $$ s(t) \, \, = \, \, t^3 \, + \, 2 t^2 \, - \, 6t \, + \, 9 \, . $$

Exercise 4: Antiderivatives 2.0

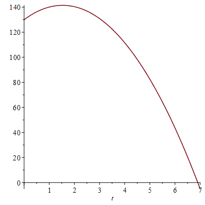
A ball is thrown upward with a speed of $15$ $m/s$ from the edge of a cliff $130$ $m$ above the ground. Find its height above the ground $t$ seconds later. When does it reach its maximum height? When does it hit the ground?

Hint (please, click on the "+" sign to read more) Find acceleration (which must be negative) by dividing $v(t)$ by $t$; find $C$ by substituting $0$ in $v(t)$; we know that $s'(t) = v(t)$ and once you find $s(t)$ by antidifferentiation by quadratic formula you can the time it takes for the ball to hit the ground

Solution (please, click on the "+" sign to read more) $v(t) = -9.8t + 15$; it reaches maximum height at $1.5$ seconds; it hits ground in $6.9$ seconds

Solution Path (please, click on the "+" sign to read more) The motion is vertical and we choose the positive direction to be upward. At time $t$ the distance above the ground is $s(t)$ and the velocity $v(t)$ is decreasing. Therefore the acceleration must be negative and we have $$ a(t) \, \, = \, \, \frac{\textrm{d} v}{\textrm{d} t} \, \, = \, \, -9.8 \, . $$ Taking antiderivatives, we have $$ v(t) \, \, = \, \, -9.8 t \, + \, C \, . $$ To determine $C$ we use the given information that $v(0) = 15$. This gives $15 = 0 + C$, so $$ v(t) \, \, = \, \, -9.8 t \, + \, 15 \, . $$ The maximum height is reached when $v(t) = 0$, that is, after $1.5$ seconds. Since $s'(t) = v(t)$, we antidifferentiate again and obtain $$ s(t) \, \, = \, \, -4.9 t^2 \, + \, 15 t \, + \, D \, . $$ Using the fact that $s(0) = 130$, we have $130 = 0 + D$ and so $$ s(t) \, \, = \, \, -4.9 t^2 \, + \, 15 t \, + \, 130 \, . $$ The expression for $s(t)$ is valid until the ball hits the ground. This happens when $s(t) = 0$, that is, when $$ -4.9 t^2 \, + \, 15 t \, + \, 130 \, \, = \, \, 0 \, , $$ or equivalently, $$ 4.9 t^2 \, - \, 15 t \, - \, 130 \, \, = \, \, 0 \, . $$ Using the quadratic formula to solve this equation, we get $$ t \, \, = \, \, \frac{15 \, \pm \, \sqrt{15^2 + 4 \cdot 4.9 \cdot 130}}{2 \cdot 4.9} \, \, = \, \, \frac{15 \, \pm \, \sqrt{2773}}{9.8} \, . $$ We reject the solution with the minus sign since it gives a negative value for $t$. Therefore the ball hits the ground after $(15 + \sqrt{2773})/ 9.8 \approx 6.9$ seconds.