
return to the main page "Calculus I for Management"
return to the page "The Fundamental Theorem of Calculus"
Worked-Out Exercises: The Fundamental Theorem of Calculus
The following set of exercises is given together with hints, solutions, and solution paths. They are designed such that
you can first try to solve them and in case you need help, please, open the "hints" section. For checking your
answer, please, open the "solution" section and for getting more details or checking your way of solving the
exercise, please, open the "solution path" section.
|
|
|
Exercise 1: Integration by Substitution Rule |
| |
|
Use the substitution rule to evaluate the integrals:
a) \({\displaystyle{ \int \, \sin(x) \sqrt{1 + \cos(x)} \, \textrm{d} x }}\)
b) \({\displaystyle{ \int \frac{x^2}{x^3 + 1} \textrm{d} x }}\)
c) \({\displaystyle{ \int \, {\rm{e}}^x \sqrt{1 + {\rm{e}}^x} \, \textrm{d} x }}\)
d) \({\displaystyle{ \int \, \sin(x) \cdot \sin(\cos(x)) \, \textrm{d} x }}\)
|
|
 Hint Hint
(please, click on the "+" sign to read more)
Substitution for Indefinite Integration:
Step 1: Choose a substitution \(u = u(x)\) that 'simplifies' the integrand \(f(x)\).
Step 2: Express the entire integral in terms of \(u\) and \(\textrm{d} u = u'(x) \textrm{d}x\). I.e. all terms involving \(x\)
and \(\textrm{d} x\) must be transformed into terms involving \(u\) and \(\textrm{d} u\).
Step 3: When step 2 is complete, the given integral should have the form
\[
\int \, f(x) \, \textrm{d} x \, \, = \, \, \int \, g(u) \, \textrm{d} u \, .
\]
If possible, evaluate this 'new' integral by finding an antiderivative \(G(u)\) for \(g(u)\).
Step 4: Replace \(u\) by \(u(x)\) in \(G(u)\) to obtain an antiderivative \(G(u(x))\) for \(f(x)\),
so that
\[
\int \, f(x) \, \textrm{d} x \, \, = \, \, G\left( u(x) \right) + C \, .
\]
|
|
 Solution Solution
(please, click on the "+" sign to read more)
a) \(\int \, \sin(x) \sqrt{1 + \cos(x)} \, \textrm{d} x = -\tfrac{2}{3} \left( 1 + \cos(x) \right)^{3/2} + C\)
b) \(\int \frac{x^2}{x^3 + 1} \textrm{d} x = \ln\left( \sqrt{|x^3 + 1|} \right) \, + \, C\)
c) \(\int \, {\rm{e}}^x \sqrt{1 + {\rm{e}}^x} \, \textrm{d} x = \tfrac{2}{3} (1 + {\rm{e}}^x)^{3/2} \, + \, C \)
d) \(\int \, \sin(x) \cdot \sin(\cos(x)) \, \textrm{d} x = -\cos\left( \cos(x) \right) + C \)
|
|
 Solution Path Solution Path
(please, click on the "+" sign to read more)
a) With the substitution \(u = 1 + \cos(x)\) and \(\textrm{d} u = -\sin(x) \textrm{d} x\) we get
\begin{eqnarray*}
\int \, \sin(x) \sqrt{1 + \cos(x)} \, \textrm{d} x
& = & - \int \, u^{1/2} \, \textrm{d} u \, \, = \, \, -\tfrac{2}{3} \, u^{3/2} + C
& = & -\tfrac{2}{3} \left( 1 + \cos(x) \right)^{3/2} + C
\end{eqnarray*}
b) With the substitution \(u = x^3 + 1\) and \(\textrm{d} u = 2 x^2 \textrm{d} x\) we get
\begin{eqnarray*}
\int \frac{x^2}{x^3 + 1} \textrm{d} x & = & \tfrac{1}{2} \int \, u^{-1} \, \textrm{d} u
\, \, = \, \,
\tfrac{1}{2} \ln|u| \, + \, C \, \, = \, \, \ln\left( \sqrt{|u|} \right) \, + \, C\\
& = &
\ln\left( \sqrt{|x^3 + 1|} \right) \, + \, C
\end{eqnarray*}
c) With the substitution \(u = 1 + {\rm{e}}^x\) and \(\textrm{d} u = {\rm{e}}^x \textrm{d} x\) we get
\begin{eqnarray*}
\int \, {\rm{e}}^x \sqrt{1 + {\rm{e}}^x} \, \textrm{d} x & = &
\int \, u^{1/2} \, \textrm{d} u \, \, = \, \, \tfrac{2}{3} u^{3/2} \, + \, C
\, \, = \, \, \tfrac{2}{3} (1 + {\rm{e}}^x)^{3/2} \, + \, C
\end{eqnarray*}
d) With the substitution \(u = \cos(x)\) and \(\textrm{d} u = -\sin(x) \textrm{d} x\) we get
\begin{eqnarray*}
\int \, \sin(x) \cdot \sin(\cos(x)) \, \textrm{d} x & = &
- \int \, \sin(u) \, \textrm{d} u \, \, = \, \, -\cos(u) + C
& = &
-\cos\left( \cos(x) \right) + C
\end{eqnarray*}
|
|
Exercise 2: Integration by Substitution Rule |
| |
|
Evaluate the following indefinite integrals:
\[
{\bf{a)}} \quad \int \, x \, \sqrt{1-x^2} \, \textrm{d} x \, , \qquad
{\bf{b)}} \quad \int \, \frac{\textrm{d} x}{4 x + 7} \, , \qquad
{\bf{c)}} \quad \int \, \frac{\cos(x)}{1 + \sin(x)} \, \textrm{d} x \, ,
\]
and
\[
{\bf{d)}} \quad \int \, \frac{{\rm{e}}^x}{(1 + {\rm{e}}^x)^2} \, \textrm{d} x \, , \qquad
{\bf{e)}} \quad \int \, \frac{(\ln(x))^2}{x} \, \textrm{d} x \, .
\]
|
|
 Hint Hint
(please, click on the "+" sign to read more)
Substitution for Indefinite Integration:
Step 1: Choose a substitution \(u = u(x)\) that 'simplifies' the integrand \(f(x)\).
Step 2: Express the entire integral in terms of \(u\) and \(\textrm{d} u = u'(x) \textrm{d}x\). I.e. all terms involving \(x\)
and \(\textrm{d} x\) must be transformed into terms involving \(u\) and \(\textrm{d} u\).
Step 3: When step 2 is complete, the given integral should have the form
\[
\int \, f(x) \, \textrm{d} x \, \, = \, \, \int \, g(u) \, \textrm{d} u \, .
\]
If possible, evaluate this 'new' integral by finding an antiderivative \(G(u)\) for \(g(u)\).
Step 4: Replace \(u\) by \(u(x)\) in \(G(u)\) to obtain an antiderivative \(G(u(x))\) for \(f(x)\),
so that
\[
\int \, f(x) \, \textrm{d} x \, \, = \, \, G\left( u(x) \right) + C \, .
\]
|
|
 Solution Solution
(please, click on the "+" sign to read more)
a) \(\int \, x \, \sqrt{1-x^2} \, \textrm{d} x = -\tfrac{1}{3} \sqrt{(1-x^2)^3} \, + \, C \)
b) \(\int \, \frac{\textrm{d} x}{4 x + 7} = \tfrac{1}{4} \cdot \ln| 4 x + 7 | \, + \, C\)
c) \(\int \, \frac{\cos(x)}{1 + \sin(x)} \, \textrm{d} x = \ln| 1 + \sin(x) | \, + \, C \)
d) \(\int \, \frac{{\rm{e}}^x}{(1 + {\rm{e}}^x)^2} \, \textrm{d} x = -\frac{1}{1+ {\rm{e}}^x} \, + \, C \)
e) \(\int \, \frac{(\ln(x))^2}{x} \, \textrm{d} x = \tfrac{1}{3} (\ln(x))^3 \, + \, C \)
|
|
 Solution Path Solution Path
(please, click on the "+" sign to read more)
a) Applying the substitution \(u = 1-x^2\) with \(\textrm{d} u = -2x \textrm{d} x\), we obtain
\begin{eqnarray*}
\int \, x \, \sqrt{1-x^2} \, \textrm{d} x & = & -\tfrac{1}{2} \int \, u^{1/2} \, \textrm{d} u
\, \, = \, \, -\tfrac{1}{2} \cdot \tfrac{2}{3} u^{3/2} \, + \, C
& = &
-\tfrac{1}{3} \sqrt{u^3} \, + \, C \, \, = \, \, -\tfrac{1}{3} \sqrt{(1-x^2)^3} \, + \, C \, .
\end{eqnarray*}
b) Applying the substitution \(u = 4 x + 7\) with \(\textrm{d} u = 4 \textrm{d} x\), we obtain
\begin{eqnarray*}
\int \, \frac{\textrm{d} x}{4 x + 7} & = & \tfrac{1}{4} \int \, u^{-1} \, \textrm{d} u
\, \, = \, \, \tfrac{1}{4} \cdot \ln|u| \, + \, C
\, \, = \, \, \tfrac{1}{4} \cdot \ln| 4 x + 7 | \, + \, C \, .
\end{eqnarray*}
c) Applying the substitution \(u = 1 + \sin(x)\) with \(\textrm{d} u = \cos(x) \textrm{d} x\), we obtain
\begin{eqnarray*}
\int \, \frac{\cos(x)}{1 + \sin(x)} \, \textrm{d} x & = & \int \, u^{-1} \, \textrm{d} u
\, \, = \, \, \ln|u| \, + \, C
& = &
\ln| 1 + \sin(x) | \, + \, C \, .
\end{eqnarray*}
d) Applying the substitution \(u = 1+ {\rm{e}}^x\) with \(\textrm{d} u = {\rm{e}}^x \textrm{d} x\), we obtain
\begin{eqnarray*}
\int \, \frac{{\rm{e}}^x}{(1 + {\rm{e}}^x)^2} \, \textrm{d} x & = & \int \, u^{-2} \, \textrm{d} u
\, \, = \, \, - u^{-1} \, + \, C
\, \, = \, \, -\frac{1}{1+ {\rm{e}}^x} \, + \, C \, .
\end{eqnarray*}
e) Applying the substitution \(u = \ln(x)\) with \(\textrm{d} u = \frac{1}{x} \textrm{d} x\), we obtain
\begin{eqnarray*}
\int \, \frac{(\ln(x))^2}{x} \, \textrm{d} x & = & \int \, u^2 \, \textrm{d} u
\, \, = \, \, \tfrac{1}{3} u^3 \, + \, C
& = &
\tfrac{1}{3} (\ln(x))^3 \, + \, C \, .
\end{eqnarray*}
|
|
Exercise 3: Area & Estimating With Finite Sums |
| |
|
Use finite approximations to estimate the area under the graph of the function
\[
f(x) \, \, = \, \, \frac{1}{x} \qquad \text{between \(x = 1\) and \(x = 5\)}
\]
using a lower sum with rectangles of equal width.
a) first two rectangles and
b) second four rectangles,
and using rectangles each of whose height is given by the value of the function at the midpoint of the rectangle's base (the midpoint rule), using
c) first two rectangles and
d) second four rectangles.
|
|
 Hint Hint
(please, click on the "+" sign to read more)
For a) and b) use lower sum rule and the midpoint rule for c) and d)
|
|
 Solution Solution
(please, click on the "+" sign to read more)
a) \(1.0\overline{6}\)
b) \(1.28\overline{3}\)
c) \(1.5\)
d) \(1.574603175\)
|
|
 Solution Path Solution Path
(please, click on the "+" sign to read more)
a) As \(f(x)\) is s.m. decreasing, we have
\[
\int^5_1 \, \frac{\textrm{d} x}{x} \, \, \approx \, \, \frac{5-1}{2}\left( \frac{1}{3} \, + \, \frac{1}{5} \right)
\, \, = \, \, \frac{16}{15} \, \, = \, \, 1.0\overline{6} \, .
\]
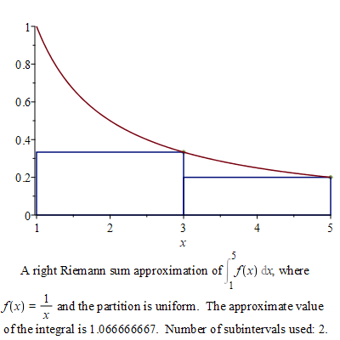
b) As \(f(x)\) is s.m. decreasing, we have
\begin{eqnarray*}
\int^5_1 \, \frac{\textrm{d} x}{x} & \approx &
\frac{5-1}{4}\left( \frac{1}{2} \, + \, \frac{1}{3} + \frac{1}{4} \, + \, \frac{1}{5} \right)
& = &
\frac{77}{60} \, \, = \, \, 1.28\overline{3} \, .
\end{eqnarray*}
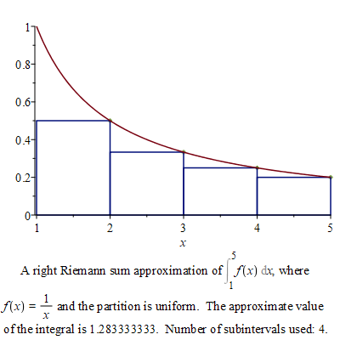
Recall,
\[
\int^5_1 \, \frac{\textrm{d} x}{x} \, \, = \, \, \Big[ \ln(x) \Big]^5_1 \, \, = \, \, \ln(5) \, \, \approx \, \, 1.609437912
\]
c) As \(f(x)\) is s.m. decreasing, we have
\[
\int^5_1 \, \frac{\textrm{d} x}{x} \, \, \approx \, \, \frac{5-1}{2}\left( \frac{1}{2} \, + \, \frac{1}{4} \right)
\, \, = \, \, \frac{3}{2} \, \, = \, \, 1.5 \, .
\]
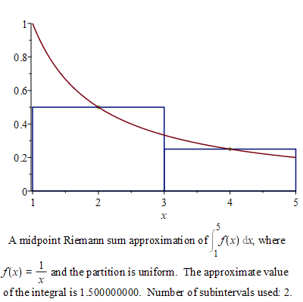
d) As \(f(x)\) is s.m. decreasing, we have
\begin{eqnarray*}
\int^5_1 \, \frac{\textrm{d} x}{x} & \approx &
\frac{5-1}{4}\left( \frac{\, \, 1 \, \,}{\tfrac{3}{2}} \, + \, \frac{\, \, 1 \, \,}{\tfrac{5}{2}} + \frac{\, \, 1 \, \,}{\tfrac{7}{2}} \, + \, \frac{\, \, 1 \, \,}{\tfrac{9}{2}} \right)
& = &
\frac{496}{315} \, \, \approx \, \, 1.574603175 \, .
\end{eqnarray*}
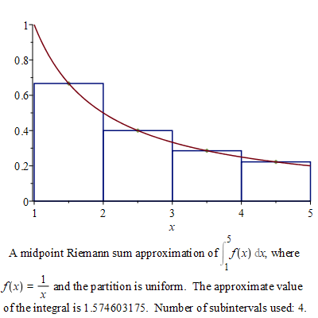
Recall,
\[
\int^5_1 \, \frac{\textrm{d} x}{x} \, \, = \, \, \Big[ \ln(x) \Big]^5_1 \, \, = \, \, \ln(5) \, \, \approx \, \, 1.609437912
\]
|
|
|
|
Copyright Kutaisi International University — All Rights Reserved — Last Modified: 12/ 10/ 2022
|
|
|

