Mathematics for Management -- Supplementary Electronic Materials

return to the main page "Calculus I for Management"
return to the page "Applications of Integration"

Worked-Out Exercises: 1st Applications of the Fundamental Theorem of Calculus

The following set of exercises is given together with hints, solutions, and solution paths. They are designed such that you can first try to solve them and in case you need help, please, open the "hints" section. For checking your answer, please, open the "solution" section and for getting more details or checking your way of solving the exercise, please, open the "solution path" section.


Exercise 1: Applying the rules for definite integrals

Suppose that \(f\) and \(g\) are integrable and that \[ \int^2_1 \, f(x) \, \textrm{d} x \, \, = \, \, -4 \, , \qquad \int^5_1 \, f(x) \, \textrm{d} x \, \, = \, \, 6 \, , \qquad \text{and} \qquad \int^5_1 \, g(x) \, \textrm{d} x \, \, = \, \, 8 \, . \] Find a) \({\displaystyle{ \int^2_2 \, g(x) \, \textrm{d} x }}\) b) \({\displaystyle{ \int^5_2 \, f(x) \, \textrm{d} x }}\) c) \({\displaystyle{ \int^5_1 \left( 4 f(x) - g(x) \right) \, \textrm{d} x }}\)

Solution (please, click on the "+" sign to read more) a) \(0\) b) \(10\) c) \(16\)

Solution Path (please, click on the "+" sign to read more) a) \(0\), because the left and right endpoint of the interval of integration are identical b) \({\displaystyle{ = \, \, \int^5_1 f(x) \, \textrm{d} x \, - \, \int^2_1 f(x) \, \textrm{d} x \, = \, 6 - (-4) \, = \, 10 }}\) c) \({\displaystyle{ = \, \, 4 \int^5_1 f(x) \, \textrm{d} x \, - \, \int^5_1 g(x) \, \textrm{d} x \, = \, 24 - 8 \, = \, 16 }}\)

Exercise 2: Applying the rules for definite integrals

Suppose that \[ \int^2_1 \, f(x) \, \textrm{d} x \, \, = \, \, 5 \, . \] Find a) \({\displaystyle{ \int^2_1 \, f(u) \, \textrm{d} u }}\) b) \({\displaystyle{ \int^2_1 \, [-f(x)] \, \textrm{d} x }}\)

Solution (please, click on the "+" sign to read more) a) \({\displaystyle{ = \, \, \int^2_1 \, f(x) \, \textrm{d} x \, \, = \, \, 5 }}\) b) \({\displaystyle{ = \, \, -\int^2_1 f(x) \, \textrm{d} x \, \, = \, \, -5 }}\)



Exercise 3: Evaluating definite integrals

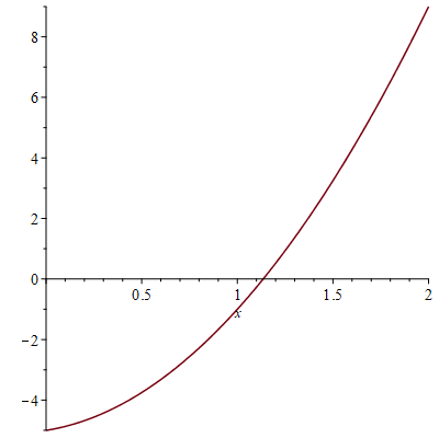
Evaluate \[ \int^2_0 \left( 3x^2 + x - 5 \right) \textrm{d} x \, . \]

Solution (please, click on the "+" sign to read more) \(0\)

Solution Path (please, click on the "+" sign to read more) We have \begin{eqnarray} \int^2_0 \left( 3x^2 + x - 5 \right) \textrm{d} x & = & \Big[ 3 \cdot \tfrac{1}{3} \cdot x^3 \, + \, \tfrac{1}{2} \cdot x^2 \, - \, 5 \cdot x \Big]^2_0 & = & \left( 8 \, + \, \tfrac{1}{2} \cdot 4 \, - \, 5 \cdot 2 \right) \, - \, \left( 0 \, + \, \tfrac{1}{2} \cdot 0 \, - \, 5 \cdot 0 \right) & = & 0 \end{eqnarray}

Exercise 4: Application of the Substitution Rule

Evaluate the following definite integrals: \[ {\bf{a)}} \quad \int^1_0 \, \cos( \tfrac{1}{2} \pi t ) \, \textrm{d} t \, , \qquad \text{and} \qquad {\bf{b)}} \quad \int^2_1 \, \frac{{\rm{e}}^{1/x}}{x^2} \, \textrm{d} x \, \, . \]

Hint (please, click on the "+" sign to read more) Apply the substitution...

Solution (please, click on the "+" sign to read more) a) \(\tfrac{2}{\pi}\) b) \({\rm{e}} - {\rm{e}}^{1/2}\)

Solution Path (please, click on the "+" sign to read more) a) Applying the substitution \(u = \tfrac{1}{2} \pi t\), \(\textrm{d} u = \tfrac{1}{2} \pi \textrm{d} t\), with \(0 \leq u \leq \tfrac{1}{2} \pi\), we obtain \[ \int^1_0 \, \cos(\tfrac{1}{2} \pi t) \, \textrm{d} t \, \, = \, \, \tfrac{2}{\pi} \int^{\tfrac{1}{2} \pi}_0 \, \cos(u) \, \textrm{d} u \, \, = \, \, \tfrac{2}{\pi} \cdot \Big[ \sin(u) \Big]^{\tfrac{1}{2} \pi}_0 \, \, = \, \, \tfrac{2}{\pi} \, . \] b) Applying the substitution \(u = {\rm{e}}^{1/x}\), \(\textrm{d} u = -x^{-2} {\rm{e}}^{1/x} \textrm{d} x\), with \({\rm{e}}^{1/2} \leq u \leq {\rm{e}}\), we obtain \[ \int^2_1 \, \frac{{\rm{e}}^{1/x}}{x^2} \, \textrm{d} x \, \, = \, \, - \int^{{\rm{e}}^{1/2}}_{{\rm{e}}} \, 1 \, \textrm{d} u \, \, = \, \, \int_{{\rm{e}}^{1/2}}^{{\rm{e}}} \, 1 \, \textrm{d} u \, \, = \, \, \Big[ u \Big]_{{\rm{e}}^{1/2}}^{{\rm{e}}} \, \, = \, \, {\rm{e}} - {\rm{e}}^{1/2} \, . \]

Exercise 5: Application of the Substitution Rule

a) If \(f\) is continuous and \(\int^4_0 f(x) \, \textrm{d} x = 10\), find \(\int^2_0 f(2x) \, \textrm{d} x\). b) If \(f\) is continuous and \(\int^9_0 f(x) \, \textrm{d} x = 4\), find \(\int^3_0 x \cdot f(x^2) \, \textrm{d} x\).

Hint (please, click on the "+" sign to read more) apply the substitution...

Solution (please, click on the "+" sign to read more) a) \(5\) b) \(2\)

Solution Path (please, click on the "+" sign to read more) a) Applying the substitution \(u = 2x\), \(\textrm{d} u = 2 \textrm{d} x\), with \(0 \leq u \leq 4\), we obtain \[ \int^2_0 \, f(2x) \, \textrm{d} x \, \, = \, \, \tfrac{1}{2} \int^4_0 \, f(u) \, \textrm{d} u \, \, = \, \, 5 \, . \] b) Applying the substitution \(u = x^2\), \(\textrm{d} u = 2x \textrm{d} x\), with \(0 \leq u \leq 9\), we obtain \[ \int^3_0 \, x \, f(x^2) \, \textrm{d} x \, \, = \, \, \tfrac{1}{2} \int^9_0 \, f(u) \, \textrm{d} u \, \, = \, \, 2 \, . \]

Exercise 6: Definite integrals and areas bounded by two curves

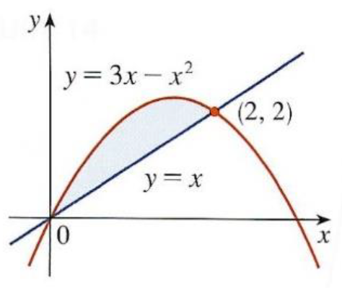
a) Set-up an integral for the area \(A\) of the shaded region. b) Evaluate the integral to find the area.

Hint (please, click on the "+" sign to read more) Use \(y = 3x-x^2\) as the upper curve and \(y = x\) as the lower curve

Solution (please, click on the "+" sign to read more) We have \begin{eqnarray} A & = & \int^2_0 \left( (3x-x^2) - x \right) \textrm{d} x \, \, = \, \, \int^2_0 \left( 2 x - x^2 \right) \textrm{d} x & = & \Big[ x^2 - \tfrac{1}{3} x^3 \Big]^2_0 \, \, = \, \, 4 - \tfrac{8}{3} - (0 - 0) \, \, = \, \, \tfrac{4}{3} \, . \end{eqnarray}



Exercise 7: Definite integrals and areas (horizontal approximation)

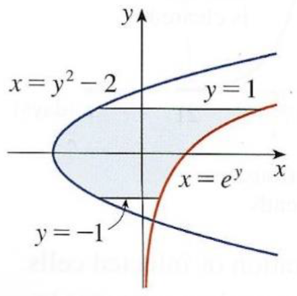
a) Set-up an integral for the area \(A\) of the shaded region. b) Evaluate the integral for find the area.

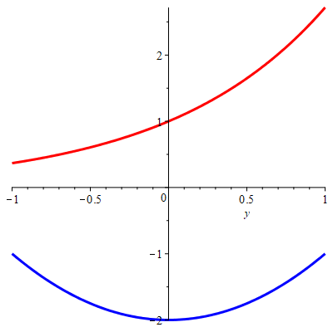
Hint (please, click on the "+" sign to read more) Use \(x = y^2 - 2\) as the left-hand curve and \(x = e^y\) as the right-hand curve

Solution (please, click on the "+" sign to read more) \[ A \, \, = \, \, \int_{-1}^1 \left( {\rm{e}}^y - (y^2 - 2) \right) \textrm{d} y \, \, = \, \, {\rm{e}}^1 - {\rm{e}}^{-1} + \tfrac{10}{3} \]

Solution Path (please, click on the "+" sign to read more) Here, the functions are already given in terms of the variable \(y\) such that we use it for integration as well. The 'upper' function is given by \(x = {\rm{e}}^y\) and the 'lower' function is given by \(x = y^2 - 2\). The boundaries of integration are \(y = -1\) and \(y=1\). Thus, \[ A \, \, = \, \, \int_{-1}^1 \left( {\rm{e}}^y - (y^2 - 2) \right) \textrm{d} y \] Moreover, \begin{eqnarray} A & = & \int_{-1}^1 \left( {\rm{e}}^y - (y^2 - 2) \right) \textrm{d} y \, \, = \, \, \int_{-1}^1 \left( {\rm{e}}^y - y^2 + 2 \right) \textrm{d} y & = & \Big[ {\rm{e}}^y - \tfrac{1}{3} y^3 + 2 y \Big]^1_{-1} \, \, = \, \, {\rm{e}}^1 - \tfrac{1}{3} + 2 - \left( {\rm{e}}^{-1} + \tfrac{1}{3} - 2 \right) & = & {\rm{e}}^1 - {\rm{e}}^{-1} + 4 - \tfrac{2}{3} \, \, = \, \, {\rm{e}}^1 - {\rm{e}}^{-1} + \tfrac{10}{3} & \approx & 5.683736 \end{eqnarray}

Exercise 8: Definite integrals and areas (vertical approximation)

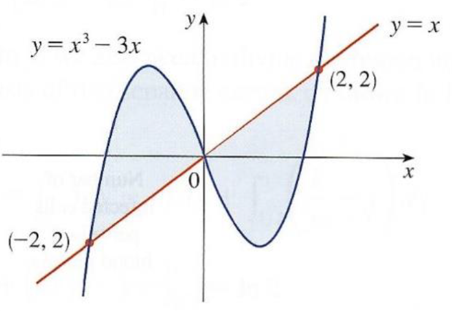
Find the area \(A\) of the shaded region.

Hint (please, click on the "+" sign to read more) Use vertical approximation (upper & lower curves) together with symmetry of the areas

Solution (please, click on the "+" sign to read more) \(8\)

Solution Path (please, click on the "+" sign to read more) Due to symmetry we have \begin{eqnarray} A & = & 2 \cdot \int^2_0 \left( x - (x^3-3x) \right) \textrm{d} x \, \, = \, \, 2 \cdot \int^2_0 \left( 4 x - x^3 \right) \textrm{d} x & = & 2 \cdot \Big[ 2 x^2 - \tfrac{1}{4} x^4 \Big]^2_0 \, \, = \, \, 2 \cdot \left( 8 - 4 - (0 - 0) \right) & = & 8 \, . \end{eqnarray}

Exercise 9: Definite integrals and areas

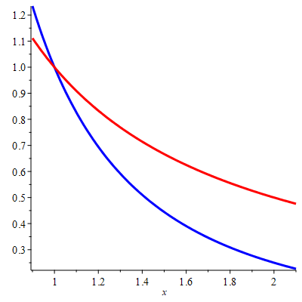
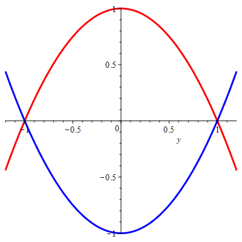
Sketch the region enclosed by the given curves. Decide whether to integrate with respect to \(x\) or \(y\). Draw a typical approximating rectangle and label its height and width. Then find the area \(A\) of the region. a) \(y = 1/x\), \(y = 1/x^2\), \(x = 2\). b) \(x = 1-y^2\), \(x = y^2 - 1\).

Hint (please, click on the "+" sign to read more) a) use \(y = 1/x\) as the upper curve and \(y = 1/x^2\) as the lower curve b) think of a y-x-coordinate system or use \(x = y^2-1\) as left-hand side curve and \(x = 1-y^2\) as right-hand side curve

Solution (please, click on the "+" sign to read more) a) upper curve: \(y = 1/x\) lower curve: \(y = 1/x^2\) b) upper curve: \(x = 1-y^2\) lower curve: \(x = y^2-1\)

Solution Path (please, click on the "+" sign to read more) a) We have \begin{eqnarray} A & = & \int^2_1 \left( \tfrac{1}{x} - \tfrac{1}{x^2} \right) \textrm{d} x \, \, = \, \, \Big[ \ln(x) - (-x^{-1}) \Big]^2_1 & = & \Big[ \ln(x) + x^{-1} \Big]^2_1 \, \, = \, \, \ln(2) + \tfrac{1}{2} - 0 - 1 \, \, = \, \, \ln(2) - \tfrac{1}{2} \end{eqnarray} b) Due to symmetry, we have \begin{eqnarray} A & = & \int^1_{-1} \left( (1-y^2) - (y^2-1) \right) \textrm{d} y \, \, = \, \, 4 \cdot \int^1_0 \left( 1 - y^2 \right) \textrm{d} y & = & 4 \cdot \Big[ y - \tfrac{1}{3} y^3 \Big]^1_0 \, \, = \, \, 4 \cdot \left(1 - \tfrac{1}{3} \right) \, \, = \, \, \tfrac{8}{3} \, . \end{eqnarray}

Exercise 10: Areas enclosed by two curves

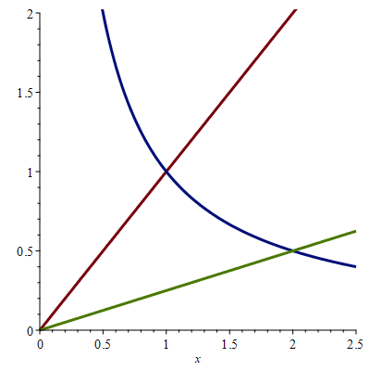
Sketch the region enclosed by the given curves and find its area \(A\). a) \(y = \sqrt{x-1}\), \(x-y=1\). b) \(y = 1/x\), \(y=x\), \(y = \tfrac{1}{4} x\), \(x > 0\).

Hint (please, click on the "+" sign to read more) a) use \(y = (x-1)^1/2\) as the upper curve and \(y = x-1\) as the lower curve b) find the intersection points of the three curves and observe that two of the curves serve as upper curve depending on the value of \(x\). The lower curve is always \(y = 1/4x\)

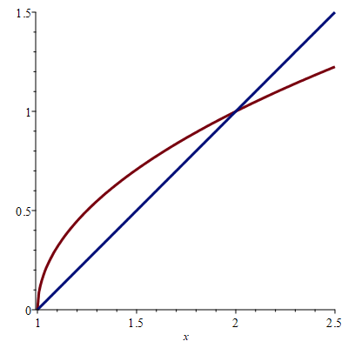
Solution (please, click on the "+" sign to read more) a) \(A = \tfrac{1}{6} \) b) \( A = \ln(2) + \tfrac{1}{4} \)

Solution Path (please, click on the "+" sign to read more) a) From the figure, and especially the domain of \(y = \sqrt{x-1}\), we have that \(x = 1\) is the lower boundary. The upper boundary is obtained from \begin{eqnarray} \sqrt{x-1} \, \, = \, \, x-1 & \Longrightarrow & x-1 \, \, = \, \, x^2 - 2x + 1 & \Longrightarrow & 0 \, \, = \, \, x^2 - 3x + 2 & \Longrightarrow & 0 \, \, = \, \, (x-1) (x-2) \end{eqnarray} We have \begin{eqnarray} A & = & \int^2_1 \left( \sqrt{x-1} - (x-1) \right) \textrm{d} x \, \, = \, \, \int^1_0 \left( u^{1/2} - u \right) \textrm{d} u & = & \Big[ \tfrac{2}{3} u^{3/2} - \tfrac{1}{2} u^2 \Big]^1_0 \, \, = \, \, \tfrac{2}{3} - \tfrac{1}{2} & = & \tfrac{1}{6} \end{eqnarray} b) From the figure we see that we will have to split the area computation into tow parts, one with \(y = x\) (red line) being the upper function and the other with \(y = \tfrac{1}{x}\) (blue line) being the upper function. In both cases the lower function is \(y = \tfrac{1}{4} x\). The intersection of \(y = x\) and \(y = \tfrac{1}{x}\) for \(x > 0\) is determined as follows: \[ x \, \, = \, \, \tfrac{1}{x} \quad \Longrightarrow \quad x^2 \, \, = \, \, 1 \quad \Longrightarrow \quad x \, \, = \, \, 1 \, . \] Next, the intersection of \(y = \tfrac{1}{x}\) and \(y = \tfrac{1}{4} x\) is determined as follows \[ \tfrac{1}{x} \, \, = \, \, \tfrac{1}{4} x \quad \Longrightarrow \quad 4 x^2 \, \, = \, \, 1 \quad \Longrightarrow \quad x \, \, = \, \, 2 \, . \] Thus, we have \begin{eqnarray} A & = & \int^1_0 \left( x - \tfrac{1}{4} x \right) \textrm{d} x \, + \, \int^2_1 \left( \tfrac{1}{x} - \tfrac{1}{4} x \right) \textrm{d} x & = & \Big[ \tfrac{1}{2} x^2 - \tfrac{1}{8} x^2 \Big]^1_0 \, + \, \Big[ \ln(x) - \tfrac{1}{8} x^2 \Big]^2_1 & = & \tfrac{3}{8} + \ln(2) - \tfrac{2}{8} - (0 - \tfrac{1}{8}) \, \, = \, \, \ln(2) + \tfrac{2}{8} & = & \ln(2) + \tfrac{1}{4} \, \, \approx \, \, 0.9431472 \end{eqnarray}

Exercise 11: Equal partitioning

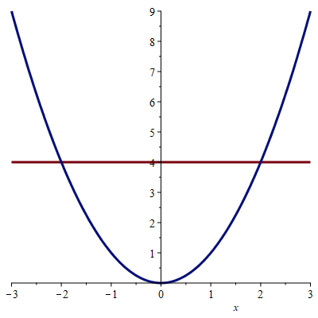
Find the number \(b\) such that the line \(y = b\) divides the region bounded by the curves \(y = x^2\) and \(y=4\) into two regions with equal area.

Hint (please, click on the "+" sign to read more) Due to symmetry, we use integration with respect to \(y\) such that the defining equation for \(b\) becomes \[ \int_0^b \, \sqrt{y} \, \textrm{d} y \, \, = \, \, \int_b^4 \, \sqrt{y} \, \textrm{d} y \]

Solution (please, click on the "+" sign to read more) \(b = 4^{2/3} \, \, \approx \, \, 2.519842\)

Solution Path (please, click on the "+" sign to read more) Due to symmetry, we use integration with respect to \(y\) such that the defining equation for \(b\) becomes \[ \int_0^b \, \sqrt{y} \, \textrm{d} y \, \, = \, \, \int_b^4 \, \sqrt{y} \, \textrm{d} y \] Hence \begin{eqnarray} \tfrac{2}{3} b^{3/2} \, \, = \, \, \tfrac{2}{3} 4^{3/2} - \tfrac{2}{3} b^{3/2} & \Longrightarrow & b^{3/2} \, \, = \, \, \tfrac{1}{2} 4^{3/2} \, \, = \, \, 4 & \Longrightarrow & b \, \, = \, \, 4^{2/3} \, \, \approx \, \, 2.519842 \end{eqnarray}

Exercise 12: Definite integrals with the same value

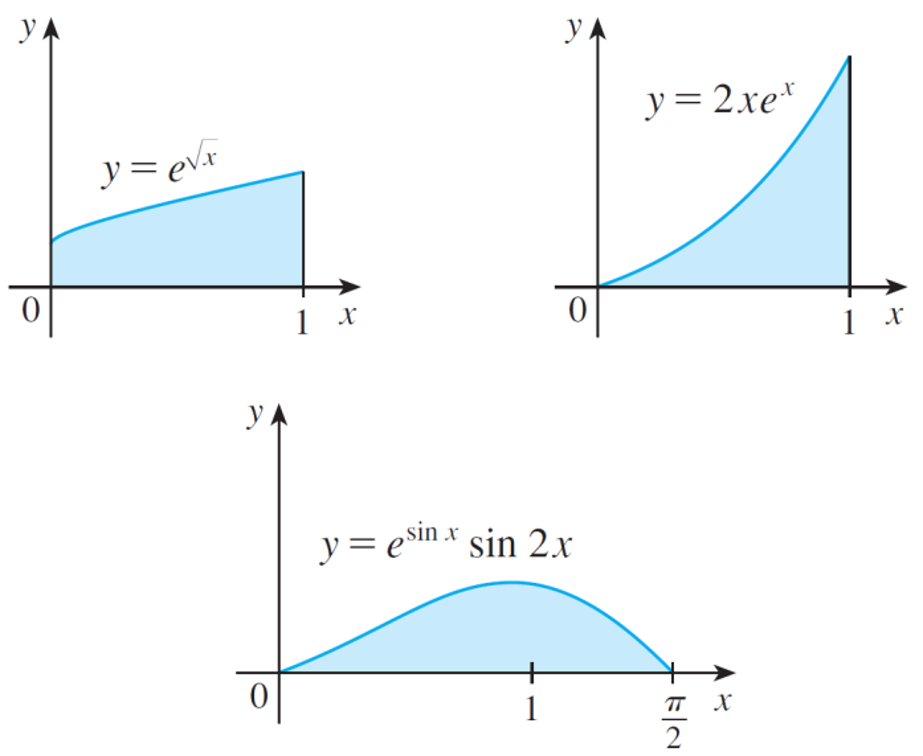
Which of the following areas are equal? Why? \[ \int^1_0 \, {\rm{e}}^{\sqrt{x}} \, \textrm{d} x \, , \qquad \int^1_0 \, 2 x {\rm{e}}^x \, \textrm{d} x \, , \] and \[ \int^{\pi/2}_0 \, {\rm{e}}^{\sin(x)} \sin(2x) \, \textrm{d} x \]

Hint (please, click on the "+" sign to read more) a) Use \(sin(2x) = 2sin(x)cos(x)\) and the substitution \(u = sin(x)\) b) Use the substitution \(u = \sqrt{x}\) c) For evaluating \(\int^1_0 2 x {\rm{e}}^x \textrm{d} x\) integration by parts is required

Solution (please, click on the "+" sign to read more) All areas are equal:

Solution Path (please, click on the "+" sign to read more) With \(\sin(2x) = 2 \sin(x) \cos(x)\) , \(u := \sin(x)\) and \(\textrm{d} u = \cos(x) \textrm{d} x\) we have \begin{eqnarray} \int^{\pi/2}_0 \, {\rm{e}}^{\sin(x)} \sin(2x) \, \textrm{d} x & = & \int^1_0 \, 2 u {\rm{e}}^u \textrm{d} u \, \, = \, \, \int^1_0 \, 2 x {\rm{e}}^x \textrm{d} x \end{eqnarray} With \(u := \sqrt{x}\) and \(\textrm{d} u = \frac{1}{2 \sqrt{x}} \textrm{d} x\) we have \begin{eqnarray} \int^1_0 \, {\rm{e}}^{\sqrt{x}} \, \textrm{d} x & = & \int^1_0 \, {\rm{e}}^{\sqrt{x}} \, \frac{2 \, \sqrt{x}}{1} \, \frac{1}{2 \, \sqrt{x}} \textrm{d} x & = & \int^1_0 \, 2 u {\rm{e}}^u \textrm{d} u \, \, = \, \, \int^1_0 \, 2 x {\rm{e}}^x \textrm{d} x \end{eqnarray} Finally, by a method called integration by parts we have: \begin{eqnarray} \int^1_0 \, 2 x {\rm{e}}^x \textrm{d} x & = & \Big[ 2 x {\rm{e}}^x \Big]^1_0 - \int^1_0 \, 2 {\rm{e}}^x \textrm{d} x \, \, = \, \, \Big[ 2 {\rm{e}}^x (x-1) \Big]^1_0 & = & 2 {\rm{e}} \end{eqnarray}